Феррари метод конечных элементов

Добавил пользователь Евгений Кузнецов
Обновлено: 20.09.2024

Метод конечных элементов

Метод конечных элементов в геомеханике

Метод конечных элементов в задачах динамики

Метод конечных элементов в механике разрушения

Применение метода конечных элементов в расчётах конструкций автомобильной техники

Метод конечных элементов

Теория метода конечных элементов

Введение в метод конечных элементов

Применение метода конечных элементов

Метод конечных элементов в задачах строительной механики летательных аппарат

Метод конечных элементов. Основы

Метод конечных элементов и САПР

Векторный метод конечных элементов: Учебное пособие

Метод конечных элементов в статике, динамике и устойчивости пространственных тонкостенных подкрепленных конструкций

Метод конечных элементов в проектировании транспортых сооружений

Расчеты машиностроительных конструкций методом конечных элементов. Справочник

Метод конечных элементов в задачах строительной механики летательных аппаратов

Введение в метод конечных элементов статики тонких оболочек

Метод конечных элементов в теории оболочек и пластин

Метод конечных элементов

Метод конечных элементов в статике и динамике тонкостенных конструкций

Метод конечных элементов

Метод конечных элементов в технике

Метод конечных элементов в механике жидкости

Метод конечных элементов для уравнений с частными производными

Введение в метод конечных элементов

Кулон. Метод конечных элементов и САПР

Применение метода конечных элементов

Теория метода конечных элементов

Метод конечных элементов для эллиптических задач

Многосеточные методы конечных элементов

Метод конечных элементов. Основы

Метод конечных элементов в технике

Метод конечных элементов в расчете деталей тепловых двигателей

Численные методы анализа и метод конечных элементов

Метод конечных элементов в расчетах тепловых двигателей

Расчет задач машиностроения методом конечных элементов. Уч. Пос

Метод конечных элементов для уравнений с частными производными

Введение в метод конечных элементов

Метод конечных элементов в задачах строительной механики летательных аппаратов

Метод конечных элементов в технике

Метод конечных элементов. Основы

Применение метода конечных элементов

Метод конечных элементов в механике железобетона

Применение метода конечных элементов

Численные методы анализа и метод конечных элементов

Метод конечных элементов. Основы

SolidWorks / COSMOSWorks. Инженерный анализ методом конечных элементов

Метод конечных элементов в нелинейных расчетах пространственных ЖБК

Метод конечных элементов в теории оболочек и пластин

Метод конечных элементов в нелинейных задачах инженерной механики

Метод конечных элементов в проектировании транспортных сооружений

Метод конечных элементов в теории сооружений и в механике сплошных сред

Метод конечных элементов в технике

Расчет ЖБК методом конечных элементов

Применение метода конечных элементов

Метод конечных элементов в технике

Введение в метод конечных элементов

СТРОИТЕЛЬНАЯ МЕХАНИКА. Специальный курс. Применение метода конечных элементов

Метод конечных элементов в расчетах прочности

Метод конечных элементов. Основы. (перевод с английского)

Метод конечных элементов в расчетах судовых конструкций

Метод конечных элементов в задачах теплопроводности

Расчет произвольной плоской стержневой системы методом конечных элементов: Методические указания

Решение задач теплопроводности методом конечных элементов в CAE-системе ELCUТ

Расчет фермы методом конечных элементов: Методические указания

Применение метода конечных элементов в механике сплошных сред: Учебно-методическое пособие

Метод конечных элементов

Метод граничных элементов в прикладных науках

Задачи контактного взаимодействия элементов конструкций

Non-Linear Finite Element Analysis of Solids and Structures: Advanced Topics

Mesh Free Methods: Moving Beyond the Finite Element Method

FINITE ELEMENT ANALYSIS .Theory and Application with ANSYS

Numerical Grid Generation. Foundations and Applications

The finite element method. Solid mechanics

Nonlinear Finite Elements in Design

МКЭ. Статья из Соросовского образовательного журнала

Basic Structured Grid Generation: With an introduction to unstructured grid generation

Finite Element Analysis: Thermomechanics of Solids

Finite Element Analysis with Error Estimators: An Introduction to the FEM and Adaptive Error Analysis for Engineering Students

Finite Element Method

Finite Element Methods and Their Applications

Finite Element Methods for Flow Problems

Finite Element Techniques for Fluid Flow

Finite Elements Using Maple: A Symbolic Programming Approach

Higher-Order Finite Element Methods

Nonlinear Stability of Finite Volume Methods for Hyperbolic Conservation Laws: and Well-Balanced Schemes for Sources

Numerical Solution of Partial Differential Equations by the Finite Element Method

Structural Analysis with Finite Elements

Finite Element Method: A Practical Course

The Finite Element Method for 3D Thermomechanical Applications - Guido Dhond

The Finite Element Method using MATLAB

The Theory of Difference Schemes - Alexander A. Samarskii

Расчет электромагнитных полей с помощью программного комплекса Ansys

Решение контактных задач в ANSYS 6.1.2003

Показаны далеко не все результаты, удовлетворяющие вашему запросу. Чтобы увидеть другие результаты, пожалуйста, уточните запрос.

Книга известных зарубежных специалистов (Канада, Великобритания), в которой представлены математические и инженерные аспекты метода конечных элементов в решении задач электродинамики и электротехники. Рассматривается практическая реализация данного метода при решении конкретных инженерных задач. Для радиоинженеров, инженеров-электриков, аспирантов и студентов инженерных электротехнических специальностей.

Предисловие редактора перевода.
Предисловие.
Треугольные элементы первого порядка для двумерных задач.
Представление электромагнитных полей.
Треугольные элементы для скалярного уравнения Гельмгольца.
Конечные элементы для интегральных операторов.
Дифференциальные операторы для ферромагнетиков.
Трехмерные задачи.
Численное решение уравнений метода конечных элементов.
Приложение.
Литература.
Предметный указатель.

Смотри также

Айфичер Э., Джервис Б. Цифровая обработка сигналов. Практический подход

М.: ИД "Вильямс", 2004. — 992 с. Данная книга предназначена в первую очередь для практиков — инженеров-электронщиков, программистов, людей, занимающихся техникой связи, вычислительными и электронными устройствами. Хотя теоретические основы и изложены в необходимом объеме (не зная основных принципов, работать с цифровыми системами невозможно), основной акцент все же делается на.

11,87 МБ
дата добавления неизвестна
изменен 13.06.2017 07:00

Андреевская Т.М. Полный курс основы аналоговой схемотехники

М.: Кафедра РЭ, МИЭМ, 2005. — 108 с. Введение. Основы полупроводниковой электроники. Контактные явления. Полупроводниковые материалы. Чистые полупроводники. Полупроводники n - и p - типа. Электронно - дырочный переход. Электронно - дырочный переход без внешнего воздействия. Электронно - дырочный переход при внешнем воздействии. Пробой p-n -перехода. Емкость p-n -перехода.

2,33 МБ
дата добавления неизвестна
изменен 14.12.2017 02:22

Воскресенский Д.И., Канащенков A.И. (ред.) Активные фазированные антенные решетки

5,50 МБ
дата добавления неизвестна
изменен 27.03.2018 04:54

Григорьев Л.Н. Цифровое формирование диаграммы направленности в фазированных антенных решетках

3,27 МБ
дата добавления неизвестна
изменен 27.03.2018 15:25

Гринев А.Ю., Гиголо А.И. Математические основы и методы решения задач электродинамики

7,35 МБ
добавлен 21.12.2015 23:42
изменен 23.12.2017 01:20

Дорф Р., Бишоп Р. Современные системы управления

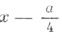
- метод сведения решения уравнения 4-й степени к решению одного кубического и двух квадратных уравнений; найден Л. Феррари (L. Ferrari, опубл. 1545). Ф. м. для уравнения y 4 + ay 3 + by 2 + cy + d =0 состоит в следующем. При помощи подстановки у= данное уравнение приводится к уравнению

не содержащему члена с х 3 . Вводя вспомогательный параметр левую часть уравнения (1) можно преобразовать по формуле

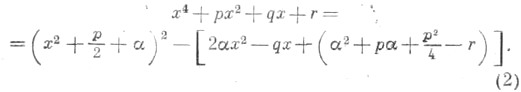
Затем подбирается значение так, чтобы выражение в квадратных скобках было полным квадратом. Для этого нужно, чтобы дискриминант квадратного трехчлена был равен нулю. Это дает для кубическое уравнение

Пусть - один из корней этого уравнения. При многочлен в квадратных скобках в (2) имеет один двукратный корень
что приводит к уравнению

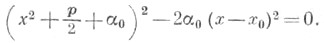
Это уравнение 4-й степени распадается на два квадратных уравнения. Корни этих уравнений и служат корнями уравнения (1).

Лит.:[1] Курош А. Г., Курс высшей алгебры, 11 изд., М., 1975.
И. В. Проскуряков.

Математическая энциклопедия. — М.: Советская энциклопедия . И. М. Виноградов . 1977—1985 .

Смотреть что такое "ФЕРРАРИ МЕТОД" в других словарях:

Метод Феррари — аналитический метод решения алгебраического уравнения четвёртой степени. Содержание 1 Описание метода 2 Вывод 3 История … Википедия

АЛГЕБРАИЧЕСКОЕ УРАВНЕНИЕ — уравнение вида где многочлен n й степени от одного или нескольких переменных . А. у. с одним неизвестным наз. уравнение вида: Здесь п целое неотрицательное число, наз. коэффициентами уравнения и являются данными, хназ. неизвестным и является… … Математическая энциклопедия

АЛГЕБРА — часть математики, посвященная изучению алгебраических операций. Исторический очерк. Простейшие алгебраич. операции арифметич. действия над натуральными и положительными рациональными числами встречаются в самых ранних математич. текстах,… … Математическая энциклопедия

ГАЛУА ТЕОРИЯ — в наиболее общем смысле теория, изучающая те или иные математич. объекты на основе их групп автоморфизмов. Так, напр., возможны Г. т. полей, колец, топологич. пространств и т. п. В более узком смысле под Г. т. понимается Г. т. полей. Возникла эта … Математическая энциклопедия

ЕСТЕСТВЕННАЯ ТЕОЛОГИЯ — [лат. theologia naturalis], термин, очерчивающий особую область философско богословских размышлений и исследований, общей характерной чертой к рых является признание в качестве отправного факта того, что всякий человек естественным образом… … Православная энциклопедия

Автомобиль — (Cars) Содержание Содержание 1. История создания первого авто 2. История марок Aston Martin Bentley Bugatti Cadillac Chevrolet Dodge Division Ferrari Ford Jaguar 3. Классификация По назначению По размеру По типу кузова По рабочему объему… … Энциклопедия инвестора

Уравнения Максвелла — Классическая электродинамика … Википедия

Уравнение четвёртой степени — График многочлена 4 ой степени с четырьмя корнями и тремя критическими точками. Уравнение четвёртой степени в математике алгебраическое уравнение вида: Четвёртая степень для алгебраических уравнений является наивысшей, при которой… … Википедия

Ювентус — У этого термина существуют и другие значения, см. Ювентус. Ювентус … Википедия

Ювентус Турин — Ювентус Полное название Juventus Football Club S.p.A. Прозвища Vecchia Signora (Старая Сеньёра), Bianconeri (Чёрно белые), Zebre (зебры). Основан … Википедия

Если — произвольный корень кубического уравнения

(резольвенты основного уравнения), то четыре корня исходного уравнения находятся как корни двух квадратных уравнений

где подкоренное выражение в правой части является полным квадратом. Отметим, что дискриминанты исходного уравнения (1) четвёртой степени и уравнения (2) совпадают.

Представим уравнение четвёртой степени в виде:

Его решение может быть найдено из следующих выражений:

+ , " width="" height="" />
- + , " width="" height="" />
+ - + , " width="" height="" />
если , тогда, решив и, сделав подстановку " width="" height="" />
, найдём корни: \pm_s\sqrt<-\alpha\pm_t\sqrt<\alpha^2-4\gamma>\over 2>,\qquad\beta=0" width="" height="" />
. - \gamma, " width="" height="" />
+ - , " width="" height="" />
\pm \sqrt\over 4>+\over 27>>" width="" height="" />
, (любой знак квадратного корня подойдёт) " width="" height="" />
, (три комплексных корня, один из которых подойдёт) \alpha +U + \beginU=0 &\to -\sqrt[3]\\U\ne 0 &\to <-P\over 3U>\end, " width="" height="" />
" width="" height="" />
+ < \pm_s W \pm_t \sqrt<-\left(3\alpha + 2 y \pm_s <2\beta\over W>\right) >\over 2 >." width="" height="" />
Два ±_s должны иметь одинаковый знак, ±_t — независимы. Для того, чтобы найти все корни, надо найти x для знаковых комбинаций ±_s,±_t = +,+ для +,− для −,+ для −,−. Двойные корни появятся два раза, тройные корни — три раза и корни четвёртого порядка — четыре раза. Порядок корней зависит от того, какой из кубических корней U выбран.

Вывод

Пусть имеется уравнение вида:

$\ x^4+ax^2+bx+c =0$

Обозначим корни уравнения как . В канонической форме будет выполняться соотношение

$\ x_1+ x_2+ x_3+ x_4=0:$

Учитывая мнимость по меньшей мере двух корней можно представить корни как:

$\ x_1=W+iK$
$\ x_2=W-iK$
$\ x_3=-W+iV$
$\ x_4=-W-iV$

Причём W,V –действительные числа. Выразим a через корни уравнения

$\ a= x_1x_2+ x_1x_3+ x_1x_4+ x_2x_3+ x_2x_4+ x_3x_4= x_1x_2+(x_1+ x_2)(x_3+x_4)+ x_3x_4=$
$\ =(W^2+K^2)+ (W^2+V^2)-4W^2= V^2+K^2-2W^2$

Выразим К через остальные коэффициенты:

$\ K^2=a+2W^2- V^2$
$\ c= x_1x_2x_3x_4 =W^4+( V^2+K^2)W^2+K^2V^2= W^4+2W^4+aV^2+2W^2V^2- V^4+aW^2$

$\ V^4-(a+ 2W^2) V^2 +c-3W^4 - aW^2=0$

)" width="" height="" />
" width="" height="" />

$\ b^2=2W^2*( a^2-4c+ 8aW^2+16 W^4)$

Или

$\ 32 W^6 +16aW^4+2(a^2-4c) W^2-b^2=0$

Отсюда

$\ y=W^2$

Заменяя получаем резольвенту, решив которую , находим W

История

С 15 лет Луиджи Феррари был учеником у миланского математика Джероламо Кардано и быстро обнаружил выдающиеся способности. К этому времени Кардано уже был известен алгоритм решения кубических уравнений; Феррари сумел найти аналогичный способ для решения уравнений четвёртой степени. Оба алгоритма Кардано опубликовал в своей книге "Высокое искусство".

Метод конечных элементов (МКЭ) — численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела (сопромата), теплообмена, гидродинамики и электродинамики.

Содержание

Идея метода

Суть метода следует из его названия. Область, в которой ищется решение дифференциальных уравнений, разбивается на конечное количество подобластей (элементов). В каждом из элементов произвольно выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (узлах) является решением задачи и заранее неизвестны. Коэффициенты аппроксимирующих функций обычно ищутся из условия равенства значения соседних функций на границах между элементами (в узлах). Затем эти коэффициенты выражаются через значения функций в узлах элементов. Составляется система линейных алгебраических уравнений. Количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов и ограничивается только возможностями ЭВМ. Так как каждый из элементов связан с ограниченным количеством соседних, система линейных алгебраических уравнений имеет разрежённый вид, что существенно упрощает её решение.

С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти, для численного анализа системы позволяет рассматривать его как одну из конкретных ветвей диакоптики — общего метода исследования систем путём их расчленения.

Иллюстрация метода на одномерном примере

Функция на с нулевыми значения на концах (голубая), и аппроксимация этой функции отрезками (красная).

Базисные функции v_k (голубые) и линейная комбинация из них, которая аппроксимирует искомую функцию (красная).

Пусть в одномерном пространстве Р1 необходимо решить следующее одномерное дифференциальное уравнение для нахождения функции на промежутке от 0 до 1. На границах области, значение функции равно 0:

$\mbox< P1 ></p> <p>:\begin u$

где известная функция, неизвестная функция от . вторая производная от по . Решение поставленной задачи методом конечных элементов разобьём на 2 этапа:

Переформулируем граничную задачу в так называемую слабую (вариационную) форму. На этом этапе вычислений почти не требуется.
На втором этапе разобьём слабую форму на конечные отрезки-элементы.

После этого возникает проблема нахождения системы линейных алгебраических уравнений, решение которой аппроксимирует искомую функцию.

Если есть решение, то для любой гладкой функции , которая удовлетворяет граничным условиям в точках и , можно записать следующее выражение:

$\int_0^1 f(x)v(x) \, dx = \int_0^1 u$

(1)

С помощью интегрирования по частям преобразуем выражение (1) к следующей форме:

Оно получено с учётом того, что .

Разобьём область, в которой ищется решение

такое, что

на конечные промежутки, и получим новое пространство :

(3) такое, что

где кусочная область пространства . Есть много способов для выбора функций . Выбираем такую , чтобы оно представлялось прямыми линиями (полиномами первой степени):

$v_<k></p> <p>(x)=\begin \over x_k\,-x_> & \mbox < if >x \in [x_,x_k], \\ \,-x \over x_\,-x_k> & \mbox < if >x \in [x_k,x_], \\ 0 & \mbox< otherwise>,\end$

для (в данном примере )

Преимущества и недостатки

Метод конечных элементов сложнее в реализации метода конечных разностей. У МКЭ, однако, есть ряд преимуществ, проявляющихся на реальных задачах: произвольная форма обрабатываемой области; сетку можно сделать более редкой в тех местах, где особая точность не нужна.

История развития метода

Возникновение метода конечных элементов связано с решением задач космических исследований в 1950-х годах. Идея МКЭ была разработана в СССР ещё в 1936 году [источник не указан 1083 дня] , но из-за неразвитости вычислительной техники метод не получил развития, поэтому впервые был применён на ЭВМ лишь в 1944 году Аргирисом. Этот метод возник из строительной механики и теории упругости, а уже затем было получено его математическое обоснование. Существенный толчок в своём развитии МКЭ получил в 1963 году после того, как было доказано то, что его можно рассматривать как один из вариантов распространённого в строительной механике метода Рэлея — Ритца, который путём минимизации потенциальной энергии сводит задачу к системе линейных уравнений равновесия. После того, как была установлена связь МКЭ с процедурой минимизации, он стал применяться к задачам, описываемым уравнениями Лапласа или Пуассона. Область применения МКЭ значительно расширилась, когда было установлено (в 1968 году), что уравнения, определяющие элементы в задачах, могут быть легко получены с помощью вариантов метода взвешенных невязок, таких как метод Галёркина или метод наименьших квадратов. Это сыграло важную роль в теоретическом обосновании МКЭ, так как позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений.

С развитием вычислительных средств возможности метода постоянно расширяются, также расширяется и класс решаемых задач. Практически все современные расчёты на прочность проводят, используя МКЭ.

Системы анализа, основанные на методе

Наиболее распространёнными вычислительными системами, основанными на методе конечных элементов являются:

Читайте также: