Как найти лямбда уилкса

Обновлено: 06.07.2024

Дискриминантный анализ — это статистический метод, предназначенный для изучения отличий между двумя или большим количеством групп объектов с использованием данных о разнообразии нескольких признаков, отличающих эти объекты друг от друга. Типичная для дискриминантного анализа задача — определение тех признаков, которые лучше всего дискриминируют (отличают) объекты, относящиеся к разным группам. После того, как определены наилучшие способы дискриминации имеющихся групп (т.е. проведена интерпретация отличий между ними), этот способ анализа позволяет проводить классификацию образцов, принадлежность которых к той или иной группе заранее неизвестна. Дискриминантный анализ разработал Рональд Фишер (1890—1962), классик биометрии и эволюционной биологии.

Пояснить, как может быть использован дискриминантный анализ, проще всего на примерах. Предположим, нас интересуют различия между женскими и мужскими скелетами (или между формой тела диплоидных и триплоидных зеленых лягушек). Мы рассматриваем совокупность скелетов мужчин и женщин (или морфологических признаков диплоидов и триплоидов) и определяем, какие признаки лучше всего дискриминируют эти группы. После этого мы можем использовать полученные нами результаты для того, чтобы определить половую принадлежность скелетов, пол которых нам изначально не известен (или определять плоидность лягушек по форме их тела).

Алгоритм дискриминантного анализа рассматривает многомерное пространство признаков, в котором расположены изучаемые объекты (состояние признаков каждого объекта определяет его положение в таком пространстве). В этом пространстве выбирается такая каноническая дискриминантная функция, которая в наибольшей степени отражает различия между группами объектов. Эта процедура напоминает процедуру, используемую при анализе главных компонент, за тем исключением, что при компонентном анализе выбираются главные компоненты, на которые проецируется максимум информации о разнообразии всех объектов, а дискриминантный анализ максимизирует отличия между заранее заданными их группами. После того, как выбрана первая такая функция, на основании оставшейся информации выбирается вторая каноническая дискриминантная функция.

С другой стороны, дискриминантный анализ близок к дисперсионному. Его задачу можно сформулировать так. В ходе дискриминантного анализа выбирается дискриминантная функция (переменная или линейное сочетание переменных) которая позволяет отличать группы друг от друга и значение которой может быть использовано для того, чтобы предсказать, к какой группе принадлежит каждый объект. Ситуацию можно рассмотреть и в терминологии одномерного дисперсионного анализа (ANOVA). Являются ли статистически значимыми отличия групп по характерным для них значениям дискриминантной функции? По какой из дискриминантных функций отличия между группами оказываются наиболее статистически значимыми?

Как выбрать дискриминантную функцию таким образом, чтобы она лучше всего отражала различия между группами? Дискриминантная функция тем лучше, чем плотнее объекты каждой группы расположены вокруг центроидов ("центров тяжести") групп, и чем дальше отстоят центроиды друг от друга. Каждая следующая функция будет вносить все меньший и меньший вклад в дискриминацию рассматриваемых групп. Каждая дискриминантная функция — это некая линейная комбинация дискриминантных переменных, т.е. признаков, характеризующих рассматриваемые объекты. Максимальное количество дискриминантных функций на единицу меньше количества дискриминантных переменных и не превышает количества групп.

Алгоритм дискриминантного анализа основан на двух достаточно важных предположениях. Принимается, что дискриминантные переменные имеют нормальное распределение, и что их дисперсия и ковариация в разных группах является однородной. Небольшие отклонения от математической истинности этих условий являются вполне допустимыми.

"Наиболее важным критерием правильности построенного классификатора является практика". Халафян, 2007

10.2. Пример выполнения дисперсионного анализа: морфометрические признаки лягушек

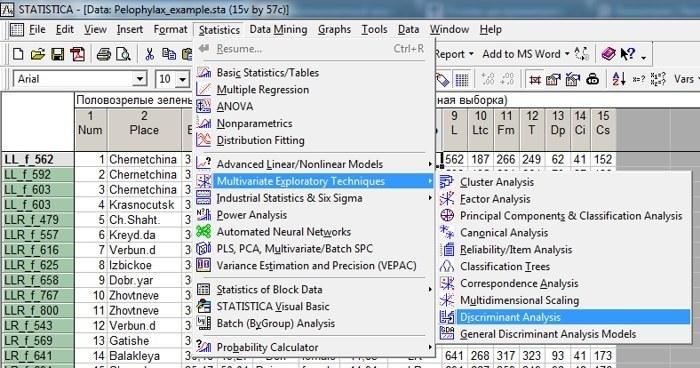
Освоить процедуру дисперсионного анализа проще всего, использовав ее для анализа данных в файле Pelophylax_example.sta. Установим, какие переменные лучше всего осуществляют дискриминацию между лягушками, относящимися к пяти разным генотипам. Для этого воспользуемся модулем Discriminant Analysis в подменю Multivariate Exploratory Techniques из меню Statistics, как это показано на рис. 10.2.1.

Рис. 10.2.1. Вызов модуля дискриминантного анализа

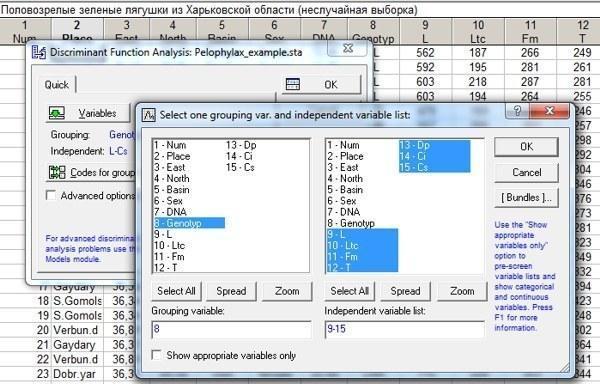
Начнем с того, что рассмотрим все семь морфометрических признаков, включенных в наш анализ. Выберем их в окне Variables так, как это показано на рис. 10.2.2.

Рис. 10.2.2. Выбор группирующей переменной (генотип) и дискриминантных переменных

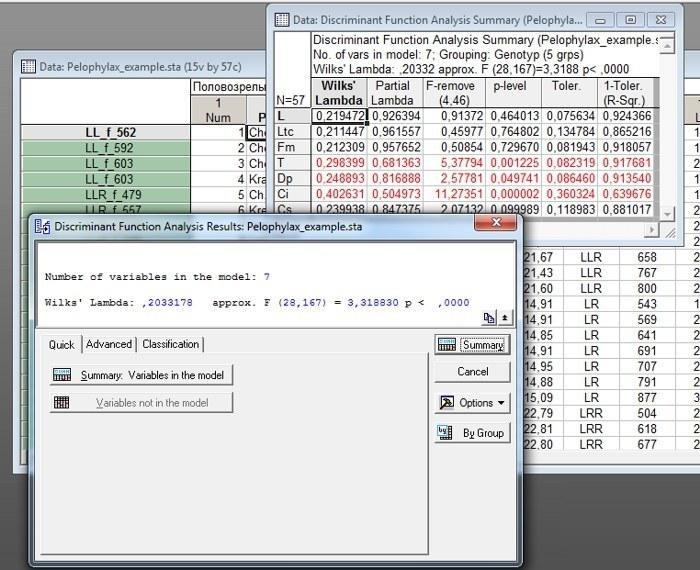
В данном случае выполним анализ с настройками по умолчанию. Его результат показан на рис. 10.2.3.

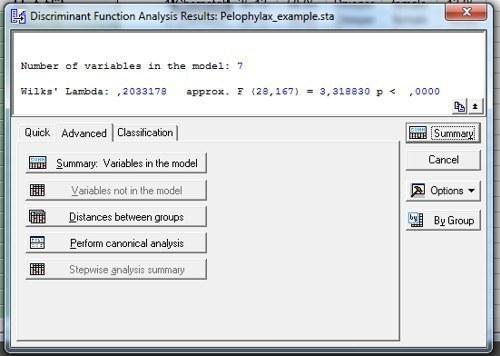
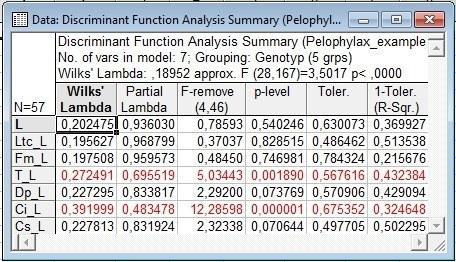
Рис. 10.2.3. После того, как на показанном на предыдущем рисунке диалоге была нажата кнопка OK, появилось окно Discriminant Function Analysis Result. Если в этом окне нажать кнопку Summary, появится таблица с результатами: Discriminant Function Analysis Summary, тоже показанная на этом рисунке

Сейчас следует рассмотреть основные статистики, которые используются для интерпретации результатов дискриминантного анализа. Самые главные из них показаны в верхней части окна Discriminant Function Analysis Result, а более подробные результаты, касающиеся каждой из переменных, отражаются в окне Discriminant Function Analysis Summary (рис. 10.2.3).

Wilk`s Lambda — лямбда Уилкса (статистика Уилкса). Эта статистика вычисляется как отношение детерминанта матрицы внутригрупповых дисперсий (ковариаций) к детерминанту общей ковариационной матрицы. Вникать в детали того, что это означает, мы не будем, и обойдемся простым определением. Лямбда Уилкса — это отношение меры внутригрупповой изменчивости к мере общей изменчивости. Внутригрупповая изменчивость — часть общей, и это означает, что лямбда Уилкса может принимать значения от 0 (группы полностью однородны) до 1 (разделение объектов на группы не приводит к тому, что внутригрупповая изменчивость оказывается меньше общей). Итого, чем меньшее значение имеет лямбда Уилкса, тем лучшим оказывается разделение на группы при дискриминантном анализе.

В верхней части окна Discriminant Function Analysis Result показано общее значение лямбды Уилкса для дискриминантного анализа с учетом всех задействованных переменных. В первом столбце окна Discriminant Function Analysis Summary, напротив каждой из переменных, показано значение лямбды Уилкса для анализа, в котором данная переменная не используется. Если исключение какой-то переменной из анализа привело к существенному ухудшению результата, то мы можем утверждать, что эта переменная вносила в него важный вклад. Итого: чем выше значение лямбды Уилкса в первом столбце окна Discriminant Function Analysis Summary, тем важнее этот признак, а чем ниже общее значение этой статистики, показанной в Discriminant Function Analysis Result, тем качественнее было проведено разделение групп. Постарайтесь не запутаться!

Partial Lambda — частная лямбда. Эта статистика показывает отношение лямбды Уилкса после добавления данной переменной к лямбде Уилкса до добавления переменной. Если переменная вносит хотя бы какой-то вклад в разделение групп, после ее добавления лямбда Уилкса должна уменьшиться. В связи с этим, чем меньшим оказывается значение частной лямбды, тем ценнее данный признак.

F-remove — F-критерий, связанный с исключением данного признака из анализа, а p-level — это уровень его статистической значимости. Если исключение признака приводит к статистически значимому изменению соотношения дисперсий, значит этот признак вносит важный вклад в дискриминацию групп.

Наконец, Toler. — толерантность. Это мера избыточности признака, которая вычисляется, как 1-R 2 , где R 2 — коэффициент множественной корреляции данного признака со всеми остальными признаками, использованными в анализе. Чем ниже толерантность, тем сильнее данный признак связан со всеми остальными. А вот для коэффициента множественной корреляции, который указывается в последнем столбце, ситуация противоположная. Чем выше R 2 , тем сильнее данный признак связан с остальными, использованными в модели.

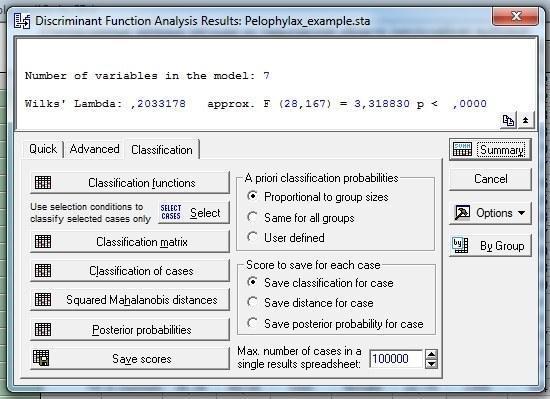
Еще одной важной мерой, позволяющей оценить качество разделения объектов по группам, является процент корректно классифицированных объектов. Чтобы узнать его, надо в коне Discriminant Function Analysis Result перейти на закладку Classification (рис. 10.2.4).

Рис. 10.2.4. Закладка Classification в окне Discriminant Function Analysis Result. Чтобы оценить корректность полученного в результате анализа распределения по группам, надо нажать на кнопку Classification Matrix (см. следующий рисунок)

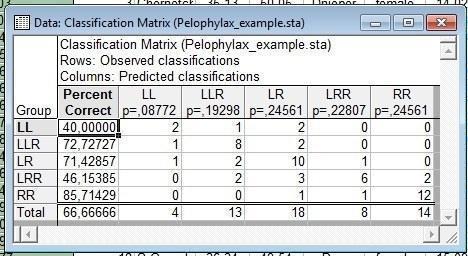
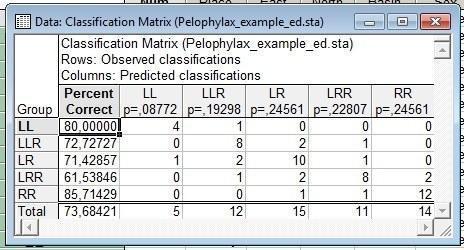
Рис. 10.2.5. Корректность классификации по использованным в анализе данным. Строки — то, к каким группам в действительности относятся рассматриваемые особи. Столбцы — отражение того, как эти объекты были бы классифицированы (по использованным переменным), если бы то, к каким группам они принадлежат, было бы неизвестным

На рис. 10.2.5 мы можем увидеть, что наш анализ позволил бы правильно определить две трети из рассмотренных особей. Лучше всего определяются особи с генотипом RR (Pelophylax ridibundus), а хуже всего LL — (Pelophylax lessonae).

Однако особенности человеческого восприятия таковы, что никакие статистики (для которых приходится запоминать, увеличение или уменьшение их свидетельствует о возрастании качества разделения) не сравнятся с наглядным графиком, показывающим распределение объектов друг относительно друга. Чтобы получить наглядную картинку, следует выполнить канонический анализ (рис. 10.2.6).

Рис. 10.2.6. В закладке Advanced в окне Discriminant Function Analysis Result можно вызвать канонический анализ (Perform canonical analysis)

Рис. 10.2.7. Окно с результатами канонического анализа. В нем нужно перейти на закладку Canonical scores (канонические корни).

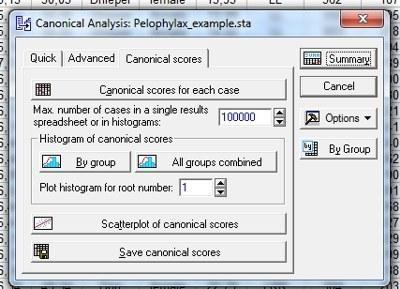
Рис. 10.2.8. . и нажать на кнопку Scatterplot of canonical scores

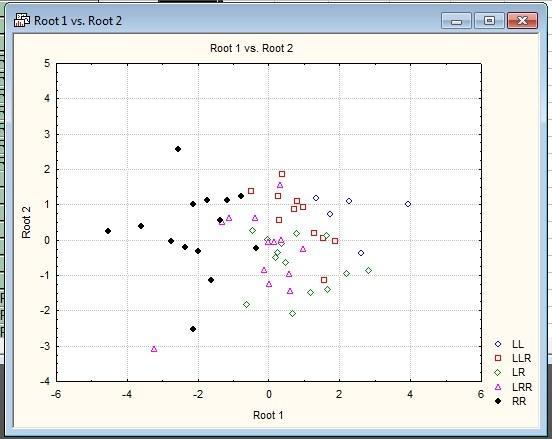
Рис. 10.2.9. Выбрав необходимые канонические корни (обычно — первый и второй), можно увидеть, как располагаются в их пространстве исследованные образцы

Полученную картину уже можно интерпретировать. Мы можем увидеть, что первый канонический корень отражает отличия между Pelophylax ridibundus и Pelophylax lessonae. Гибриды располагаются между родительскими видами, "выстроившись" в порядке отношения родительских геномов. Разделение не абсолютное и включает определенное перекрывание (именно с ним связаны случаи, когда классификация была бы выполнена некорректно).

Напомню, что канонические корни — это те самые канонические дискриминантные функции, которые выбираются так, чтобы они наилучшим образом отражали отличия между группами объектов. Эти корни являются линейными комбинациями дискриминантных переменных (в предельном случае — соответствуют каким-то из переменных). Чтобы посмотреть, как связаны канонические корни и дискриминантные переменные надо нажать на кнопку Factor structure на вкладке Advanced в окне Canonical Analisis. Там показаны коэффициенты корреляции, связывающие каждый канонический корень с каждой дискриминантной переменной.

10.3. Поиск более эффективных способов разделения групп

В предыдущем пункте в дискриминантном анализе использовались "сырые" морфометрические признаки. Можно предположить, что это не самое лучшее решение. Виды и внутривидовые формы животных очень часто отличаются друг от друга пропорциями — соотношениями разных морфометрических признаков. Во многих случаях в зоологических исследованиях удачным оказывается такой вариант: использовать некий признак, который характеризует общий размер, в его абсолютной форме, а все остальные — в виде пропорций, их отношения к признаку, характеризующему размер. В нашем примере, естественно, размер характеризует признак L — длина тела. Шесть остальных признаков можно использовать в виде пропорций — частного от деления их абсолютных размеров на L. Выполним анализ с таким набором признаков. Его результаты показаны на рис. 10.3.1.

Рис. 10.3.1. Результаты дискриминантного анализа, в котором использовалась длина тела и отношения других признаков к длине тела. Обозначениям наподобие T_L соответствуют пропорции, которые вычисляются как T/L

При использовании абсолютных значений признаков лямбда Уилкса была равна 0,20. При переходе к пропорциям она немного уменьшилась, и стала равной 0,19 (0,18952).

Рис. 10.3.2. Корректность классификации при использовании отношений морфометрических признаков к длине тела

Немного улучшилась и корректность классифицирования. Она теперь составляет 73,7% (при использовании "сырых" данных была 66,6%).

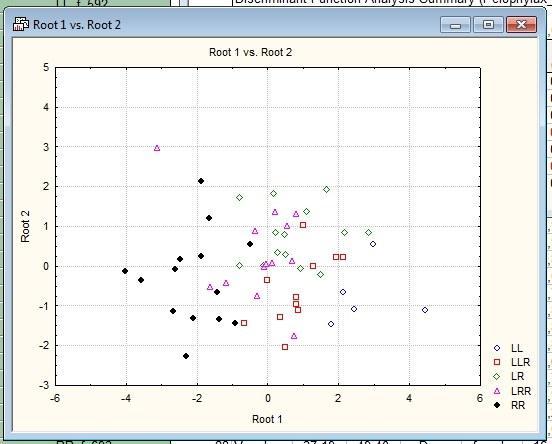
Рис. 10.3.3. Распределение изучаемых объектов в плоскости двух первых канонических дискриминантных функций при использовании данных о длине тела особей и отношениям их промеров к длине тела

Качество разделения особей на плоскости двух канонических корней изменилось несущественно.

Нам не удалось качественно улучшить качество классифицирования, но мы убедились, что используя вместо сырых данных их соотношения, мы можем улучшить результат. А как найти оптимальный набор признаков, который надо использовать для поиска различий между представителями разных генотипов?

В задачах построения объяснительных моделей часто встает вопрос о нахождении критерия, по которому можно было бы классифицировать данные (построение дискриминирующей функции) и определить переменные, которые различают две или более возникающие совокупности (группы).

Например, некий исследователь в области образования может захотеть исследовать, какие переменные относят выпускника средней школы к одной из трех категорий: (1) поступающий в колледж, (2) поступающий в профессиональную школу или (3) отказывающийся от дальнейшего образования или профессиональной подготовки. Для этой цели исследователь может собрать данные о различных переменных, связанных с учащимися школы.

После выпуска большинство учащихся естественно должно попасть в одну из названных категорий.

Затем можно использовать Дискриминантный анализ для определения того, какие переменные дают наилучшее предсказание выбора учащимися дальнейшего пути.

Пусть имеется n наблюдений, разбитых на k групп (классов).

Каждое наблюдение характеризуется набором из m значений (независимые переменные). Также для каждого наблюдения известно, к какой из k групп оно принадлежит. Принадлежность объектов к разным классам выражается в том, что для объектов данного класса имеет распределение , j=1,…,k.

Задача состоит в том, чтобы для нового наблюдения определить группу (класс), к которой оно принадлежит.

Дискриминантный анализ предполагает, что являются m-мерными нормальными распределениями , j=1,…,k и имеющими плотности:

, j=1,…,k (1)

Здесь - m-мерный вектор средних значений, а - невырожденная ковариационная матрица ().

В таком случае, исходя из принципа максимального правдоподобия, будем считать областью притяжения закона множество таких наблюдений , где плотность распределения больше других. См. рис. 1.

В данном примере, где графики плотности пересекаются только в одной точке, получается, что вся прямая разбивается на 2 области притяжения.

Рис. 1. Области притяжения для k=2, m=1

Это равносильно тому, что линейно связанная с логарифмом плотности величина:

, j=1,…,k (2)

имеет наименьшее значение среди . Таким образом, n+1 наблюдение будет отнесено к i-группе, если (x)- имеет наименьшее значение.

Оценка качества дискриминации

Рассмотрим модель Фишера, которая является частным случаем нормальной дискриминантной модели при .

При k =2 нетрудно проверить, что поверхность, задаваемая условием , разделяет два класса уравнением:

Линейную функцию часто называют дискриминантной функцией, как функцию, описывающую гиперплоскость, по которой разделяются две группы. Мы же будем под дискриминантной функцией понимать линейную часть функции (x).

Обозначим через расстояние Махаланобиса между и . Чем более далекими в метрике Махаланобиса являются и , тем меньше вероятность ошибочной классификации.

В общем случае, . Расстояние Махаланобиса является мерой расстояния между двумя точками x и y в пространстве, определяемым двумя или более коррелированными переменными. Можно заметить, что в случае, когда переменные не коррелированны (), расстояние Махаланобиса совпадет с евклидовым.

При k>2 с помощью гиперплоскостей m–мерное пространство разбивается на k частей. В каждой из них содержится только одна точка из – та, к которой все точки данной части находятся ближе, чем к остальным в смысле расстояния Махаланобиса. См. рис. 2.

Рис. 2. Области притяжения для k=3, m=2

Для проверки гипотезы о равенстве средних в качестве статистик критерия используют статистики Уилкса (лямбда Уилкса):

Здесь T = – общая матрица рассеяния, матрица внутриклассового разброса: ,

где - матрица рассеяния j-го класса.

Очевидно, что ее значение меняется от 1.0 (нет дискриминации) до 0.0 (полная дискриминация).

Оказывается, что верно матричное тождество:

где R = – матрица разброса между элементами класса, – число элементов в j-м классе.

При выполнении гипотезы :

имеет распределение Фишера.

отклоняется (т.е. дискриминация значима), если

где - квантиль уровня .

Описание данных и постановка задачи

Имеется файл с данными boston.sta с ценами земельных участков в Бостоне. Всего в файле содержится 1012 участков (наблюдений).

Участок характеризуется 11 параметрами ORD1,…, ORD11 – непрерывные предикторы, а также одной группирующей категориальной переменной PRICE – характеризующий ценовой класс, к которому относиться данный участок (HIGH, MEDIUM, LOW). См. рис. 3.

Рис. 3. Таблица с исходными данными boston.sta

Цель: определить критерий, по которому можно классифицировать наблюдения по категории PRICE в зависимости от параметров участка (ORD1-ORD11), и, c его помощью, определить категорию PRICE для нового наблюдения.

Решение задачи по шагам

Для решения задачи перейдем на вкладку Анализ/Многомерный Разведочный анализ/Дискриминантный анализ. См. рис. 4.

В качестве группирующей переменной укажем переменную PRICE, в качестве независимых – переменные ORD1-ORD11. Анализ будем проводить пошагово. Количество шагов соответствует числу переменных.

Пошаговый анализ с включением/исключением на каждой итерации при помощи статистики Фишера определяет, стоит ли включать в модель соответствующую переменную.

Обычно в пошаговом анализе дискриминантной функции, переменные включают в модель, если соответствующее им значение F больше, чем значение F-включить, переменные удаляют из модели, если соответствующее им значение F меньше, чем значение F-исключить.

Заметим, что значение F-включить всегда должно быть больше, чем значение F-исключить. Если при проведении пошагового анализа с включением, вы пожелаете включить все переменные, установите в поле F-включить значение, равное очень маленькому числу (например, 0.0001), а в поле F-исключить значение 0.0.

Если при проведении пошагового анализа с исключением, вы пожелаете исключить все переменные из модели, установите в поле F-включить значение, равное очень большому числу (например, 0.9999), а в поле F-исключить чуть-чуть меньшее значение того же порядка (например, 0.9998).

Рис. 4. Пошаговый дискриминантный анализ

Нажмем кнопку ОК.

В следующем меню на вкладке Дополнительно установим опцию: Пошаговый с включением с F-вкл = 10 и вывод результатов на каждом шаге.

Нажмем кнопку ОК. См. рис. 5.

Рис. 5. Результаты анализа на 0-м шаге

Шаг 0.

Лямбда Уилкса равна 1 на 0-м шаге, т.к. никакой дискриминационной модели еще нет.

Нажмем кнопку Переменные вне модели. См. рис. 6.

Лямбда Уилкса. Значение посчитано по формуле (3) и определяет значение L, если бы соответствующая переменная была включена в модель на этом шаге.

Частная лямбда Уилкса. Эта статистика для одиночного вклада соответствующей переменной в дискриминацию между совокупностями является аналогом частной корреляции. Так как в модель еще не введено ни одной переменной, частная лямбда Уилкса равна лямбда Уилкса.

F-включить и p-значение. Считается также как и F-статистика для всей модели (формула (4)), только вместо лямбды Уилкса подставляется Частная лямбда Уилкса.

Взглянув на таблицу, вы видите, что наибольшие значения величины F-включить дает переменная ORD11 (последняя строка). Переменная с максимальным значением F-включить будет включена в модель на первом шаге (т.е. вносящая наибольший вклад в модель).

Рис. 6. Переменные вне модели на 0-м шаге

Шаг 1.

Анализ включил в модель переменную ORD11, т.к. она несет наибольший вклад среди прочих переменных в дискриминационную модель (наибольшее значение F-вкл). См. рис. 7.

Рис. 7. Результаты анализа на 1-м шаге

Нажав кнопку переменные в модели, получим следующую таблицу (рис. 8.)

Рис. 8. Переменные в модели на 1-м шаге

Далее, проводя аналогичные рассуждения, в модель будет включена переменная ORD4. См. рис. 9.

Рис. 9. Переменные в модели на 2-м шаге

Алгоритм дискриминантного анализа останавливается, если на очередном шаге F-вкл. в модель оказывается меньше заданного значения (в нашем примере F-вкл. = 10) или если на очередном шаге уже все переменные будут в модели.

В нашем случае анализ остановился на 7-м шаге (т.к. F (2, 1003) = 8,314937 < F-вкл. = 10 ). См. рис. 10.

Рис. 10. Итоги дискриминантного анализа

На вкладке Дополнительно можно вызвать пункт Итоги пошагового анализа (либо пункт Переменные в модели). См. рис. 11.

Рис. 11. Переменные, включенные модель к концу анализа

В итоге в модель было включено 7 переменных.

Кнопка Расстояние между группами выдаст таблицу с квадратами расстояний Махаланобиса между центрами групп. См. рис. 12.

Рис. 12. Квадраты расстояний Махаланобиса

Вместе с таблицей результатов расстояний Махаланобиса выводятся две другие таблицы результатов: одна с F-значениями, связанными с соответствующими расстояниями, а другая – с соответствующими p-уровнями. См. рис. 13.

Рис. 13. Значения F-статистики и p-уровней для расстояний Махаланобиса

Эти p-уровни должны интерпретироваться с осторожностью, если только в анализ не привносится сильная априорная гипотеза относительно того, какие пары групп должны показывать особенно большие (и значимые) расстояния.

Классификация

Перейдем к подменю Классификация. См. рис. 14.

Рис. 14. Подменю Классификация Дискриминантного анализа

Здесь, кроме уже описанных выше расстояний Махаланобиса (таблица с расстояниями на рис. 16), можно вывести коэффициенты функции классификации для каждой группы. См. рис. 15.

Рис. 15. Функции классификации (дискриминации)

На рис. 15 в каждом столбце находятся коэффициенты дискриминирующей функции для соответствующего класса (стоит еще раз отметить, что подразумевается линейная функция).

Рис. 16. Квадраты расстояния Махаланобиса до центров соответствующих групп

Также можно вывести матрицу классификации и классификацию наблюдений. См. рис. 17. и рис. 18.

Рис. 17. Матрица классификации

Обе таблицы основываются на результатах таблицы с квадратами расстояний Махаланобиса (см. выше).

Рис. 18. Классификация наблюдений

Стоит обратить внимание, что в предыдущих таблицах каждая группа была помечена априорной вероятностью (см. в названии переменных таблиц). Их можно задать на панели справа (См. рис. 14 и рис. 19).

Рис. 19. Априорные вероятности

Априорные вероятности отражают наши знания о природе явления перед проведением эксперимента.

Например, если мы знаем, что в начальных данных преобладают элитные земельные участки (PRICE = HIGH), то этот факт, конечно, должен повлиять на анализ, увеличивая долю наблюдений, помеченных в результате дискриминации как HIGH.

По умолчанию, в системе STATISTICA априорные вероятности задаются пропорционально размеру групп.

Вероятности, полученные после эксперимента, называются апостериорными. Они приведены в таблице на рис. 20.

Рис. 20. Апостериорные вероятности

Апостериорные вероятности связаны с априорными по следующей формуле:

где .

Литература

Рао С.Р. Линейные статистические методы и их применения, Наука 1968.

Розанов Ю.А. Теория вероятностей, случайные процессы и математическая статистика, Наука 1985.

Боровиков В.П. STATISTICA, искусство анализа данных на компьютере, Питер 2001.

Боровиков В.П. Нейронные сети. STATISTICA Neural Networks, Горячая линия – Телеком 2008.

Дискриминация (от лат. discriminatio -различение) в математической статистике – выявление различий между объектами исследования. Если общества развитых стран борются с дискриминацией, то для статистиков – это хлеб насущный.

Итак, дискриминантный анализ служит для выявления линейных зависимостей между двумя и более группами. Он является как разведочным, так и подтверждающим. То есть, мы можем как найти статистические зависимости обуславливающие различие между группами, так и использовать их для дальнейшей дискриминации других объектов.

Сам по себе дискриминантный метод является линейным методом, а потому имеет много общего с дисперсионным (ANOVA) и регрессионным методами.

Данный метод предъявляет ряд требований к данным:

Нормальность признаков
Одинаковая дисперсия признаков в группах
Различие в средних

В принципе, данными условиями можно пренебречь. Главное, что бы работало. При этом чем меньше соблюдаются условия – тем меньше будет процент верной классификации. Вот и всё.

Важно отметить, что в геохимии мы имеем дело, как правило, с нелинейными закономерностями. Но это не означает, что линейные функции подходят неудовлетворительно. По своему опыту дискриминации интрузий, аномалий и пр. объектов, – использование нейросетей для дискриминации позволяло улучшить результат всего на 2-5%.

Рис. 1. Выборка данных.

Допустим мы имеем выборку силикатных анализов трёх типов интрузий: Норильский тип - продуктивный и несёт оруденение; Зубовский – похож на Норильский, но непродуктивный; Нижнеталнахский – совсем “пустой”. Дополнительно, в выборку добавлен ряд проб с нового объекта и нам потребуется выяснить к какому типу относится он. Важно отметить, что в нашем случае, каждый тип охарактеризован разным количеством проб в силу неравномерности изучения, но никак не природной встречаемости (это важно).

Лог-нормальные данные были предварительно прологарифмированы. О том, как проверить данные на нормальность – см. ранние посты.

Рис. 2. Строим графики типа ящик-с-усами.

Данные графики показывал как строить ранее, потому у вас затруднений не должно быть.

Графики типа ящик-с-усами показывают различие в средних и дисперсии, то что нам нужно для предварительной разведки данных.

Рис. 3. График распределения оксида хрома по типам интрузий.

Типичный график с высоким различием объектом. Посмотрите, ящики Норильского и Нижнеталнахского типов не пересекаются, средние однозначно различаются. Дисперсия (ширина ящика) у Норильского типа выше, но этим можно пренебречь. Теоретически, можно проводить дискриминацию уже по оксиду хрома – посчитать необходимое количество проб, и вперед, но мы хотим большего – большей надежности и качества за счёт использования других переменных.

Рис. 4. График распределения оксида марганца по типам интрузий.

Типичный график со слабым различием между группами.

Рис. 5. Традиционный дискриминантный анализ.

Ниже есть выбор анализа General Discriminant (Общий дискриминантный). Для него доступны категориальные независимые переменные (у геохимиков, это например, название вмещающих горных пород, их возраст; у кредиторов – внешний вид заёмщика). Так же, там имеется кросс-проверка результатов. Тем не менее, выбрал “традиционный” анализ, потому что в таком случае можно еще провести канонический анализ и полнее расммотреть зависимости.

Рис. 6. Определение переменных и групп для анализа.

Рис. 7. Выбор параметров проведения анализа.

В данном случае можно выбрать один из трёх методов выбора переменных:

стандартного, когда включаются сразу все переменные;
последовательного включения, когда включаются данные у которых F больше определённого значения (уточняется в Advanced);
последовательного исключения, когда из всех переменных исключаются те, у которых значение F меньше определённого значения (выставляется в Advanced).

F значение – отношение межгрупповой дисперсии к внутригрупповой.

Рис. 8. Итоговая характеристика анализа.

Итак, из тринадцати переменных анализ выбрал одиннадцать. Последней включённой переменной оказался оксид магния с F = 2,306. Лямбда Уилкса составила 0,19, что близко к нулю и является хорошим результатом. То есть, можно ожидать выского процента верной классификации.

Рис. 9. Таблица переменных участвовавших в дискриминантном анализе.

Как видно из таблицы, максимальные различия вносят переменные оксида хрома, калия, и железа II.

Рис. 10. Результаты классификации.

Перед выводом отчётных таблиц необходимо определиться с априорными вероятностями (Apriori classification probabilities). Как говорил в самом начале, у нас количество проб не влияет на природную встречаемость интрузий, а обусловлено лишь неравномерным изучением объектов. Поэтому следует выбрать равнозначные априорные вероятности. Тем не менее, если вы имеете априорную информацию (например, встречаемость интрузий в конкретном районе, или вероятность нахождения интрузий по геофизическим данным), или хотите подстраховаться, то можно самостоятельно расставить априорные вероятности через пункт User Defined.

Затем выведем таблицы: фукнций классификации, матрицы классификаций и таблицу классификации проб. Каждая таблица зависит от априорных вероятностей.

Рис. 11. Функции классификации.

Так то тут представлены коэффициенты к дискриминантным функциям типа y=ax+b. Выигрывает тот тип, значение дискриминантной функции которого принимает максимальное значение.

Рис. 12. Матрица результатов классификации.

В строках матрицы - наблюдаемые значения, в колонках – предсказанные. Таким образом, Норильский тип чаще всего путаем с Зубовским, и реже с Нижнеталнахским.

Верная классикация происходит в 88% случаев, зная это с помощью биномиального распределения можно расчитать необходимое количество проб для дискриминации объектов.

Рис. 13. Таблица результатов классификации.

В выборку были добавлены пробы без определённого типа интрузии, но они так же были проанализированы и в большинстве своём относятся к Норильскому типу.

Рис. 14. Проведение канонического анализа.

Канонический анализ – аналогичен методу главных компонент и служит для выявления связей между двумя и более множествами переменных.

Рис. 15. Параметры канонического анализа.

Рис. 16. Тест Хи-квадрат канонических корней.

В данной таблице показываются все канонические корни и их статистическая значимость. Обращаем внимание на значимые корни. В данном случае, два корня и оба статистически значимы.

Рис. 17. Факторный анализ канонических корней.

Объяснить структуру канонических корней можно по таблице факторных нагрузок, которая аналогична одноименной в факторном анализе. Если кто сомневается, то можно подглядеть в графики типа ящик-с-усами.

Если рассмотреть данную таблицу вместе с графиков канонических значений (рис. 19), то увиидим, что чем меньше значение Lg(Cr2O3) и блольше Lg(K2O) тем больше значение Корня 1, а значит, тем более вероятнее классификация Нижнеталнахского типа. Корень 2 разделяет Норильский и Зубовский типы: чем больше SiO2, Na2O и FeO и чем меньше Fe2O3 и MgO, тем более вероятен Зубовский тип.

Получается, что для Нижнеталхнаского типа характерна калиевая специализация с обедненностью хромом, а для Норильского типа характерна хромово-магниевая специализация с повышенной окисленностью железа.

Рис. 18. Построение графика распределения канонических значений.

Рис. 19. График распределения канонических значений.

Рис. 20. Добавление средних значений на график.

Поскольку, в дискриминации всё упирается в средние значения, то логично вынести их на график. Скопируем средние значения канонических корней из соответствующей таблицы.

На графике щёлкам правой клавишей мышки и выбраем пункт “Graph Data Editor” – редактор данных графика

Рис. 21. Добавление нового графика.

В любом месте щелкаем правой клавишей мышки и выбираем пункт “Add new plot” – добавить новый график. Вставляем скопированные средние значения.

Рис. 22. Итоговый график распределения канонических значений.

Канонические корни аналогичны факторам – являются латентными призаками. То есть все отдельные особенности переменных объединяются в новые математические переменные. Они не являются доказательством определённых геохимических процессов проиходивших в недрах, но могут их отражать, потому называются латентными. Удобство сокращения тринадцати переменных в две на глазах.

Кроме всего, на графике можно посмотреть форму групп, их положение, а так же наличие ошибок в данных – если пробы отходят сильно далеко от своих групп, то скорее всего они являются ошибочно классифицированными, вплоть до определения нового типа интрузии.

На графике, например, можно увидеть отдалённые три пробы Норильского типа, которые находятся в поле Нижнеталнахского. Надо их проверить.