Параметр лямбда в гребневой регрессии

Добавил пользователь Владимир З.
Обновлено: 19.09.2024

Регрессия (англ. Regression) — метод моделирования зависимости между зависимой переменной [math]y[/math] и одной или несколькими независимыми переменными [math]x_1, x_2, \dots, x_n[/math] . В случае нескольких независимых переменных регрессия называется множественной (англ. multivariate regression). Цель регрессионного анализа состоит в том, чтобы оценить значение непрерывной выходной переменной по значениям входных переменных.

Содержание

Линейная регрессия (англ. linear regression) — разновидность регрессии для моделирования линейной зависимости между зависимой и независимой переменными.

Логистическая регрессия (англ. logistic regression) — разновидность регрессии для прогнозирования вероятности некоторого события по значениям независимых переменных. Зависимая переменная [math]y[/math] в этом случае принимает значения [math]0[/math] или [math]1[/math] (рассматриваемое событие не произошло или произошло соответственно).

Гребневая регрессия или ридж-регрессия (англ. ridge regression) — один из методов понижения размерности. Применяется для борьбы с избыточностью данных, когда независимые переменные коррелируют друг с другом, вследствие чего проявляется неустойчивость оценок коэффициентов многомерной линейной регрессии.

Рассмотрим пример линейной модели: [math]y = b_1 x_1 + b_2 x_2 + b_3 x_3 + \varepsilon[/math] . Пусть имеет место зависимость [math]x_1 = x_2 + x_ 3[/math] . Добавим к первому коэффициенту произвольное число [math]a[/math] , а из двух других коэффициентов это же число вычтем. Получаем (без случайной ошибки):

[math]y = (b_1 + a)x_1 + (b_2 - a)x_2 + (b_3 - a)x_3 = b_1 x_1 + b_2 x_2 + b_3 x_3 + a(x_1 - x_2 - x_3) = b_1 x_1 + b_2 x_2 + b_3 x_3[/math]

Несмотря на относительно произвольное изменение коэффициентов модели мы получили исходную модель, то есть такая модель неидентифицируема.

На практике чаще встречается проблема сильной корреляции между независимыми переменными. В этом случае оценки параметров модели получить можно, но они будут неустойчивыми.

Напомним задачу многомерной линейной регрессии:

Рассматривается линейная зависимость [math]f(x, \beta) = \langle \beta, x \rangle[/math] .

Находим вектор [math]\beta^*[/math] , при котором достигается минимум среднего квадрата ошибки:

[math]Q(\beta) = ||F \beta - y||^2[/math] [math]\beta^*=\arg \min\limits_\beta Q(\beta)[/math]

Методом наименьших квадратов находим решение:

[math]\beta^* = (F^T F)^ F^T y[/math]

В условиях мультиколлинеарности матрица [math]F^T F[/math] становится плохо обусловленной.

Для решения этой проблемы наложим ограничение на величину коэффициентов [math]\beta[/math] : [math]||\overrightarrow||_2^2 \leq t^2[/math] .

Функционал [math]Q[/math] с учетом ограничения принимает вид:

[math]Q_<\lambda>(\beta) = ||F \beta - y||^2 + \lambda ||\beta||^2[/math] ,

где [math]\lambda[/math] — неотрицательный параметр.

Решением в этом случае будет

[math]\beta^* = (F^T F + \lambda I_n)^ F^T y[/math]

Это изменение увеличивает собственные значения матрицы [math]F^T F[/math] , но не изменяет ее собственные вектора. В результате имеем хорошо обусловленную матрицу.

Диагональная матрица [math]\lambda I_n[/math] называется гребнем.

Точность предсказания для данного датасета и параметров:

Пример гребневой регрессии с применением smile.regression.RidgeRegression [1]

Рис.1. Сравнение Лассо- и Ридж- регрессии, пример для двумерного пространства независимых переменных.
Бирюзовые области изображают ограничения на коэффициенты [math]\beta[/math] , эллипсы — некоторые значения функции наименьшей квадратичной ошибки.

Метод регрессии лассо (англ. LASSO, Least Absolute Shrinkage and Selection Operator) похож на гребневую регрессию, но он использует другое ограничение на коэффициенты [math]\beta[/math] : [math]||\overrightarrow||_1 \leq t[/math]

Функционал [math]Q[/math] принимает следующий вид:

[math]Q_<\lambda>(\beta) = ||F \beta - y||^2 + \lambda ||\beta||[/math]

Основное различие лассо- и ридж-регрессии заключается в том, что первая может приводить к обращению некоторых независимых переменных в ноль, тогда как вторая уменьшает их до значений, близких к нулю. Рассмотрим для простоты двумерное пространство независимых переменных. В случае лассо-регрессии органичение на коэффициенты представляет собой ромб ( [math]|\beta_1| + |\beta_2| \leq t[/math] ), в случае ридж-регрессии — круг ( [math]\beta_1^2 + \beta_2^2 \leq t^2[/math] ). Необходимо минимизировать функцию ошибки, но при этом соблюсти ограничения на коэффициенты. С геометрической точки зрения задача состоит в том, чтобы найти точку касания линии, отражающей функцию ошибки с фигурой, отражающей ограничения на [math]\beta[/math] . Из рисунка 1 интуитивно понятно, что в случае лассо-регрессии эта точка с большой вероятностью будет находиться на углах ромба, то есть лежать на оси, тогда как в случае ридж-регрессии такое происходит очень редко. Если точка пересечения лежит на оси, один из коэффициентов будет равен нулю, а значит, значение соответствующей независимой переменной не будет учитываться.

Точность предсказания для данного датасета и параметров:

Пример Лассо-регрессии с применением smile.regression.LASSO [2]

Описанные выше методы никак не учитывали наличие в данных шума, тогда как в реальных данных он скорее всего будет присутствовать. Предположим, что в данных все же есть некоторый шум, и что он распределен нормально. Тогда задачу линейной регрессии можно записать в следующем виде:

[math]f(x, \beta) = \langle \beta, x \rangle + \varepsilon[/math] , где [math]\varepsilon \sim N(0, \sigma^2)[/math] .

Решением этой задачи мы и будем заниматься в этом разделе.

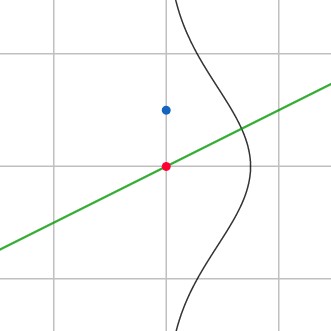
Рис.2. Регрессия и шум в данных.
Синяя точка — значение из датасета, красная — значение, полученное в результате работы алгоритма регрессии. Также на рисунке зеленой линией изображена предсказанная функция, а черной — гауссово распределение шума.

Байесовская линейная регрессия (англ. Bayesian linear regression) — подход в линейной регрессии, в котором предполагается что шум распределен нормально.

На рисунке 2 синяя точка показывает значения из датасета, красная — значение, предсказанное регрессией. Поскольку центр гауссианы находится в красной точке, маленькие отклонения синей точки от красной более вероятны, а большие менее вероятны.

Для решения поставленной задачи регрессии воспользуемся методом максимального правдоподобия.

[math]p(y|x, \beta, \sigma^2) = N(x \beta, \sigma^2)[/math] ,

где [math]p(y|x, \beta, \sigma^2)[/math] — плотность распределения значения [math]y[/math] из датасета, которая, как мы ранее предположили, соответствует нормальному распределению с центром в точке [math]x \beta[/math] (значение для [math]y[/math] , предсказанное алгоритмом).

Будем также предполагать, что данные независимы:

[math]p(y|x, \beta, \sigma^2) = \prod\limits_^n N(x_i \beta, \sigma^2)[/math]

Поскольку нас интересует только максимум, положим [math]\sigma = 1[/math] :

[math]\arg\max p(y|x, \beta) = \arg\max \prod\limits_^n N(x_i \beta, 1)[/math]

Прологарифмируем это выражение:

[math]\arg\max \ln p(y|x, \beta) = \arg\max \ln \prod\limits_^n N(x_i \beta, 1) \\ = \arg\max \ln <\left( \frac<1><(\sqrt<2 \pi>)^n> \exp<\left(-\frac<1> \sum\limits_^n (y_i - x_i \beta)^2\right)>\right )> \\ = \arg\max - \sum\limits_^n (y_i - x_i \beta)^2 \\ = \arg\min \sum\limits_^n (y_i - x_i \beta)^2[/math]

Таким образом, оказывается, что метод максимального правдоподобия с учетом шума в данных сводится к оценке по методу наименьших квадратов, которую мы уже видели в обычной линейной регрессии.

Точность предсказания для данного датасета и параметров:

Логическая регрессия (англ. logic regression) — обобщенный метод регрессии, применяемый в основном в случае, когда независимые переменные имеют двоичную природу (при этом зависимая переменная не обязательно двоичная). Задачей логической регрессии является определение независимых переменных, которые могут быть выражены как результат вычисления булевой функции от других независимых переменных.

Обычно в методах регрессии не учитывается связь между переменными. Предполагается, что влияние каждой переменной на результат не зависит от значений других переменных. Однако это предположение зачастую неверно.

Пусть [math]x_1, x_2, \dots, x_k[/math] — двоичные независимые переменные, и пусть [math]y[/math] — зависимая переменная. Будем пытаться натренировать модели регрессии вида [math]g(E(y)) = b_0 + b_1 L_1 + \dots + b_n L_n[/math] , где [math]L_j[/math] — булева функция от переменных [math]x_i[/math] (например [math]L_j = (x_2 \lor \overline) \land x_7[/math] ). Для каждого типа модели необходимо определить функцию, которая отражает качество рассматриваемой модели. Например, для линейной регрессии такой функцией может быть остаточная сумма квадратов. Целью метода логической регрессии является минимизация выбранной функции качества посредством настройки параметров [math]b_j[/math] одновременно с булевыми выражениями [math]L_j[/math] .

Рис.3. Допустимые действия в процессе роста дерева.
Элементы, появившиеся в результате применения операции, выделены черным фоном.

Может показаться не совсем понятным, как же применить регрессию к булевым выражениям. Рассмотрим в общих чертах алгоритм логической регрессии. Логическая регрессия, как и другие методы регрессии, перебирает различные выражения в попытках минимизировать функцию потерь. Для [math]k[/math] переменных можно составить [math]2^[/math] различных выражений. Нужно найти более эффективный метод для поиска наилучшего выражения, чем простой перебор всех вариантов.

Любое логическое выражение можно представить в виде дерева, где в узлах расположены операции, а листья представляют собой переменные. Будем называть такие деревья логическими деревьями (англ. logic trees). Будем называть соседями (англ. neighbours) логического дерева такие деревья, которые могут быть получены из него за один шаг. Допустимые шаги проиллюстрированы на рисунке 3.

Рассмотрим самый простой алгоритм поиска наилучшего дерева — жадный поиск (англ. greedy search).

В качестве стартового дерева выберем одну переменную, которая дает минимальное значение функции потерь среди всех остальных переменных.
Перебираем соседей текущего дерева и выбираем такое, что оно уменьшает значение функции потерь по сравнению с текущим, а также дает наименьший результат среди остальных соседей.
Если такого дерева не существует, алгоритм завершается. Если оно все же есть, выбираем его в качестве текущего и повторяем второй шаг.

Этот алгоритм склонен к переобучению, а также в некоторых ситуациях может остановиться преждевременно, так и не дойдя до наилучшего дерева. Существует также алгоритм под названием имитация отжига (англ. simulated annealing) который показывает лучшие результаты, чем описанный жадный поиск.

Проверка адекватности построенной регрессионной модели

Между значением , значением из регрессионной модели и значением тривиальной оценкой выборочного среднего существует следующее соотношение:

По сути, член в левой части определяет общую ошибку относительно среднего. Первый член в правой части () определяет ошибку, связанную с регрессионной моделью, а второй () ошибку, связанную со случайными отклонениями и необъясненной построенной моделью.

Поделив обе части на полную вариацию игреков , получим коэффициент детерминации:

Коэффициент показывает качество подгонки регрессионной модели к наблюдаемым значениям . Если , то регрессия на не улучшает качества предсказания по сравнению с тривиальным предсказанием .

Другой крайний случай означает точную подгонку: все , т.е. все точки наблюдений лежат на регрессионной плоскости.

Однако, значение возрастает с ростом числа переменных (регрессоров) в регрессии, что не означает улучшения качества предсказания, и потому вводится скорректированный коэффициент детерминации

Его использование более корректно для сравнения регрессий при изменении числа переменных (регрессоров).

Доверительные интервалы для коэффициентов регрессии. Стандартной ошибкой оценки является величина , оценка для которой

где - диагональный элемент матрицы Z. Если ошибки распределены нормально, то, в силу свойств 1) и 2), приведенных выше, статистика

распределена по закону Стьюдента с степенями свободы, и поэтому неравенство

где - квантиль уровня этого распределения, задает доверительный интервал для с уровнем доверия .

Проверка гипотезы о нулевых значениях коэффициентов регрессии. Для проверки гипотезы об отсутствии какой бы то ни было линейной связи между и совокупностью факторов, , т.е. об одновременном равенстве нулю всех коэффициентов, кроме коэффициентов, при константе используется статистика

распределенная, если верна, по закону Фишера с k и степенями свободы. отклоняется, если

где - квантиль уровня .

в начало

Описание данных и постановка задачи

Исходный файл с данными tube_dataset.sta содержит 10 переменных и 33 наблюдения. См. рис. 1.

Рис. 1. Исходная таблица данных из файла tube_dataset.sta

Этапы решения:

1) Сначала проведем разведочный анализ имеющихся данных на предмет выбросов и незначимых данных (построение линейных графиков и диаграмм рассеяния).

2) Проверим наличие возможных зависимостей между наблюдениями и между переменными (построение корреляционных матриц).

в начало

Решение задачи по шагам

Рис. 2. Диаграмма рассеяния зависимой переменной (№9) и кол-ва скважин (№8)

Цифра после символа Е в отметках по оси Х обозначает степень числа 10, которое определяет порядок значений переменной №8 (Количество скважин действующих). В данном случае речь идет о значении порядка 100.000 скважин (10 в 5 степени).

На диаграмме рассеяния на рис. 3 (см. ниже) отчетливо видно 2 облака точек, причем каждое из них имеет явную линейную зависимость.

Понятно, что переменная №1, скорее всего, войдет в регрессионную модель, т.к. нашей задачей является выявление именно линейной зависимости между предикторами и откликом.

Рис. 3. Диаграмма рассеяния зависимой переменной (№9) и Инвестиций в нефтяную промышленность (№1)

Шаг 2. Построим линейные графики всех переменных в зависимости от времени. Из графиков видно, что данные по многим переменным сильно разнятся в зависимости от номера квартала, но рост из года в год сохраняется.

Полученный результат подтверждает предположения, полученные на основе рис. 3.

Рис. 4. Линейный график 1-й переменной в зависимости от времени

В частности, на рис. 4 построен линейный график для первой переменной.

Чтобы разбить наблюдения согласно кварталам на 2 таблицы, воспользуемся пунктом Данные/Подмножество/Случайный выбор. Здесь в качестве наблюдений нам надо указать условия на значения переменной КВАРТАЛ. Cм. рис. 5.

Согласно заданным условиям наблюдения будут скопированы в новую таблицу. В строчке снизу можно указать конкретные номера наблюдений, однако в нашем случае это займет много времени.

Рис. 5. Выбор подмножества наблюдений из таблицы

В качестве заданного условия зададим:

V10 = 1 OR V10 = 4

V10 – это 10 переменная в таблице (V0 – это столбец с наблюдениями). По сути, мы проверяем каждое наблюдение в таблице, относится оно к 1-ому или 4-ому кварталу или нет. Если мы хотим, выбрать другое подмножество наблюдений, то можно либо сменить условие на:

V10 = 2 OR V10 = 3

либо перенести первое условие в исключающие правила.

Нажав ОК, мы сначала получим таблицу с данными только по 1 и 4 кварталу, а затем и таблицу с данными по 2 и 3 кварталу. Сохраним их под именами 1_4.sta и 2_3.sta через вкладку Файл/Сохранить как.

Далее будем работать уже с двумя таблицами и полученные результаты регрессионного анализа для обеих таблиц можно будет сравнить.

Шаг 4. Построим матрицу корреляций для каждой из групп, чтобы проверить предположение относительно линейной зависимости и учесть возможные сильные корреляции между переменными при построении регрессионной модели. Так как есть пропущенные данные, корреляционная матрица была построена с опцией попарного удаления пропущенных данных. См. рис. 6.

Рис. 6. Матрица корреляций для первых 9-ти переменных по данным 1 и 4 кварталов

Из корреляционной матрицы в частности понятно, некоторые переменные очень сильно коррелируют друг с другом.

Стоит отметить, что достоверность больших значений корреляции возможна только при отсутствии выбросов в исходной таблице. Поэтому диаграммы рассеяния для зависимой переменной и всех остальных переменных обязательно должны учитываться при корреляционном анализе.

Например, переменная №1 и №2 (Инвестиции в нефтяную и газовую промышленность соответственно). См. рис.7 (или, например, рис. 8).

Рис. 7. Диаграмма рассеяния для переменной №1 и №2

Рис. 8. Диаграмма рассеяния для переменной №1 и №7

Данная зависимость легко объяснима. Также ясен и высокий коэффициент корреляции между объемами добычи нефти и газа.

Высокий коэффициент корреляции между переменными (мультиколлиниарность) нужно учитывать при построении регрессионной модели. Здесь могут возникнуть большие ошибки при вычислении коэффициентов регрессии (плохообусловленная матрица при вычислении оценки через МНК).

Приведем наиболее распространенные способы устранения мультиколлиниарности:

1) Гребневая регрессия.

Данная опция задается при построении множественной регрессии. Число - малое положительное число. Оценка МНК в таком случае равна:

где Y – вектор со значениями зависимой переменной, X – матрица, содержащая по столбцам значения предикторов, а – единичная матрица порядка n+1. (n – количество предикторов в модели).

Плохообусловленность матрицы при гребневой регрессии значительно уменьшается.

2) Исключение одной из объясняющих переменных.

В этом случае из анализа исключается одна объясняющая переменная имеющая высокий парный коэффициент корреляции ( r>0.8 ) с другим предиктором.

3) Использование пошаговых процедур с включением/исключением предикторов.

Пояснение данной опции смотрите ниже.

Обычно, в таких случаях, используют либо гребневую регрессию (она задается в качестве опции при построении множественной), либо, на основе значений корреляции, исключают объясняющие переменные, имеющие высокий парный коэффициент корреляции (r > 0.8), либо пошаговую регрессию с включением/исключением переменных.

Рис. 9. Построение множественной регрессии для таблицы 1_4.sta

Множественную регрессию можно проводить пошагово. В этом случае в модель будут пошагово включаться (или исключаться) переменные, которые вносят наибольший (наименьший) вклад в регрессию на данном шаге.

Также данная опция позволяет остановиться на шаге, когда коэффициент детерминации еще не наибольший, однако уже все переменные модели являются значимыми. См. рис. 10.

Рис. 10. Построение множественной регрессии для таблицы 1_4.sta

Особо стоит отметить, что пошаговая регрессия с включением, в случае, когда количество переменных больше количества наблюдений, является единственным способом построения регрессионной модели.

Установка нулевого значения свободного члена регрессионной модели используется в случае, если сама идея модели подразумевает нулевое значение отклика, когда все предикторы окажутся равными 0. Чаще всего подобные ситуации встречаются в экономических задачах.

В нашем случае свободный член мы включим в модель.

Рис. 11. Построение множественной регрессии для таблицы 1_4.sta

В качестве параметров модели выберем Пошаговую с исключением (Fвкл = 11, Fвыкл = 10), с гребневой регрессией (лямбда = 0.1). И для каждой группы построим регрессионную модель. См. рис.11.

Результаты в виде Итоговой таблицы регрессии (см. также рис. 14) представлены на рис.12 и рис.13. Они получены на последнем шаге регрессии.

Шаг 6. Проверка адекватности модели

Обратим внимание, что, несмотря на значимость всех переменных в регрессионной модели (p-уровень < 0.05 – подсвечены красным цветом), коэффициент детерминации R2 существенно меньше у первой группы наблюдений.

Коэффициент детерминации показывает, по сути, какая доля дисперсии отклика объясняется влиянием предикторов в построенной модели. Чем ближе R2 к 1, тем лучше модель.

F-статистика Фишера используется для проверки гипотезы о нулевых значениях коэффициентов регрессии (т.е. об отсутствии какой бы то ни было линейной связи между и совокупностью факторов, , кроме коэффициента ). Гипотеза отклоняется при малом уровне значимости.

В нашем случае (см. рис. 12) значение F-статистики = 13,249 при уровне значимости p < 0,00092, т.е. гипотеза об отсутствии линейной связи отклоняется.

Рис. 12. Результаты регрессионного анализа данных по 1 и 4 кварталу

Рис. 13. Результаты регрессионного анализа данных по 2 и 3 кварталу

Шаг 7. Теперь проведем анализ остатков полученной модели. Результаты, полученные при анализе остатков, являются важным дополнением к значению коэффициента детерминации при проверке адекватности построенной модели.

Для простоты будем рассматривать лишь группу, разбитую на кварталы с номерами 2 и 3, т.к. вторая группа исследуется аналогично.

В окне, представленном на рис. 14, на вкладке Остатки/предсказанные/наблюдаемые значения нажмем на кнопку Анализ остатков, и далее нажмем на кнопку Остатки и предсказанные. (См. рис. 15)

Кнопка Анализ остатков будет активна, только если регрессия получена на последнем шаге. Чаще оказывается важным получить регрессионную модель, в которой значимы все предикторы, чем продолжить построение модели (увеличивая коэффициент детерминации) и получить незначимые предикторы.

В этом случае, когда регрессия не останавливается на последнем шаге, можно искусственно задать количество шагов в регрессии.

Рис. 14. Окно с результатами множественной регрессии для данных по 2 и 3-му кварталам

Рис. 15. Остатки и предсказанные значения регрессионной модели по данным 2 и 3 квартала

Прокомментируем результаты, представленные на рис. 15. Важным является столбец с Остатками (разница первых 2-х столбцов). Большие остатки по многим наблюдениям и наличие наблюдения с маленьким остатком может указывать на последнее как на выброс.

Другими словами анализ остатков нужен для того, чтобы отклонения от предположений, угрожающие обоснованности результатов анализа, могли быть легко обнаружены.

Рис. 16. Остатки и предсказанные значения регрессионной модели по данным 2 и 3 кварталов + 2 границы 0.95 доверительного интервала

В конце приведем график, иллюстрирующий данные, полученные из таблицы на рис. 16. Здесь добавлены 2 переменные: UCB и LCB – 0.95 верх. и нижн. дов. интервал.

UBC = V2+1.96*V6

LBC = V2-1.96*V6

И удалены четыре последних наблюдения.

Построим линейный график с переменными (Графики/2М Графики/Линейные графики для переменных)

1) Наблюдаемое значение (V1)

2) Предсказанное значение (V2)

3) UCB (V9)

4) LCB (V10)

Результат представлен на рис. 17. Теперь видно, что построенная регрессионная модель довольно неплохо отражает реальное потребление труб, особенно на результатах недавнего прошлого.

Это означает, что в ближайшем будущем реальные значения могут быть приближены модельными.

Отметим один важный момент. В прогнозировании при помощи регрессионных моделей всегда важен базовый временной интервал. В рассматриваемой задаче были выбраны кварталы.

Соответственно, при построении прогноза предсказываемые значения будут также получаться по кварталам. Если нужно получить прогноз на год, то придется прогнозировать на 4 квартала и в конце накопится большая ошибка.

Подобную проблему можно решить аналогично, вначале лишь агрегируя данные от кварталов к годам (например, усреднением). Для данной задачи подход не очень корректен, так как останется всего лишь 8 наблюдений, по которым будет строиться регрессионная модель. См. рис.18.

Рис. 17. Наблюдаемые и предсказанные значения вместе с 0.95 верх. и ниж. довер. интервалами (данные по 2 и 3 кварталам)

" />

Рис. 18. Наблюдаемые и предсказанные значения вместе с 0.95 верх. и ниж. довер. интервалами (данные по годам)

Чаще всего такой подход применяется при агрегировании данных по месяцам, при исходных данных по дням.

Следует помнить, что все методы регрессионного анализа позволяют обнаружить только числовые зависимости, а не лежащие в их основе причинные связи. Поэтому ответ на вопрос о значимости переменных в полученной модели остается за экспертом в данной области, который, в частности, способен учесть влияние факторов, возможно, не вошедших в данную таблицу.

в начало

Вывод

для 1 и 4 квартала и

для 2 и 3 квартала,

где – объем бурения эксплутационного;

– объем добычи газа;

– количество скважин действующих;

– потребление труб.

Параметры модели: Пошаговая с включением (Fвкл = 1), гребневая регрессия с параметром лямбда = 0,1.

Результат получен на последнем шаге регрессии.

Литература

Рао С.Р. Линейные статистические методы и их применения, Наука 1968.

Розанов Ю.А. Теория вероятностей, случайные процессы и математическая статистика, Наука 1985.

Боровиков В.П. STATISTICA, искусство анализа данных на компьютере, Питер 2001.

Боровиков В.П. Нейронные сети. STATISTICA Neural Networks, Горячая линия – Телеком 2008.

Есть вопросы?

Специалисты StatSoft всегда на связи.

Продукты

Разобраться в STATISTICA?

Легко!

Отраслевые решения на базе STATISTICA!

Видеоролики STATISTICA

Консалтинг StatSoft:

помощь в принятии верных решений

Big Data:

Как извлечь полезную информацию?

Актуально:

Вступление:
Ридж-регрессия (или L2-регуляризация) - это разновидность линейной регрессии. В линейной регрессии он минимизирует остаточную сумму квадратов (или RSS, или функцию стоимости), чтобы максимально соответствовать обучающим примерам. Функция стоимости также представлена буквой J

Функция стоимости для линейной регрессии:

Здесь h(x (i) ) представляет собой гипотетическую функцию для прогнозирования. y (i) представляет значение целевой переменной для i-го примера.
m - общее количество обучающих примеров в данном наборе данных.

Линейная регрессия рассматривает все функции одинаково и находит несмещенные веса, чтобы минимизировать функцию стоимости. Это может вызвать проблему переобучения (или модель не может хорошо работать с новыми данными). Линейная регрессия также не может работать с коллинеарными данными (коллинеарность относится к событию, когда функции сильно коррелированы). Короче говоря, линейная регрессия - это модель с высокой дисперсией. Итак, на помощь приходит Ridge Regression. В регрессии Риджа к функции стоимости линейной регрессии добавляется штраф l2 (квадрат величины весов). Это сделано для того, чтобы модель не переборщила с данными. Модифицированная функция стоимости для регрессии хребта приведена ниже:

Здесь w _j представляет собой вес j-го признака.
n - количество объектов в наборе данных.

Математическая интуиция:
Во время оптимизации функции стоимости градиентным спуском добавленный l2 приводит к уменьшению весов модели до нуля или близким к нулю. Из-за штрафов за веса наша гипотеза становится более простой, более обобщенной и менее склонной к переобучению. Все веса уменьшаются на один коэффициент лямбда. Мы можем контролировать степень регуляризации с помощью гиперпараметра лямбда.

Если лямбда установлена равной 0, регрессия гребня равна линейной регрессии.
Если лямбда установлена равной бесконечности, все веса уменьшаются до нуля.

Итак, мы должны установить лямбду где-то между 0 и бесконечностью.

Решение мультиколлинеарности-гребневой регрессии и LASSO

Модель множественной линейной регрессии

Результат оценки методом наименьших квадратов для :

Если есть сильная коллинеарность, то этоМежду каждым вектором-столбцом существует сильная корреляция, что приведет кЧто вызвалоЗначение по диагонали очень велико.

И разные выборки также приводят к оценкам параметровИзменения очень большие. То есть дисперсия средства оценки параметра также увеличивается, и оценка параметра будет неточной.

Итак, можно ли удалить некоторые из наиболее важных переменных? Если переменные p имеют сильную корреляцию, какие из них следует удалить?

В этой статье представлены два метода для определения того, как исключить переменные из моделей с мультиколлинеарностью. А именно регрессия гребня и LASSO (Примечание: LASSO разработан на основе регрессии гребня)

Мысль:

Поскольку коллинеарность приведет к тому, что оценки параметров станут очень большими, добавьте пару к целевой функции наименьших квадратов.Штрафная функция

При минимизации новой целевой функции также необходимо учитыватьРазмер стоимости,Не слишком большой 。

Добавьте коэффициент k к штрафной функции

По мере увеличения k влияние коллинеарности становится все меньше и меньше. В процессе увеличения коэффициента штрафной функции нарисуйте оценочные параметрыИзменение (k) - это след по гребню.

Используйте форму следа гребня, чтобы определить, хотим ли мы исключить параметр (например: след гребня сильно колеблется, указывая на то, что переменный параметр имеет коллинеарность).

Стандартизируйте данные для облегчения будущего(K) Сравнение следа гребня, иначе размеры параметров разных переменных не сопоставимы.
Создайте штрафную функцию и нарисуйте карту трассы гребня для различных k.
В соответствии с картой трассировки гребня выберите, какие переменные следует исключить.

Объективная функция регресса гребня

, где t - Функция.Чем больше, тем меньше t (здесьK)

Как показано на рисунке выше, точка касания - это решение, полученное с помощью гребневой регрессии. Это геометрический смысл регрессии гребня.

Видно, что регрессия гребня контролируетДиапазон изменения, ослабляющего коллинеарностьВлияние размера.

Расчетный результат решенной регрессии гребня:

Природа регресса гребня

. Это видно из целевой функции гребневой регрессии, Коэффициент штрафной функцииЧем больше (или k), тем выше важность штрафной функции в целевой функции.

Для оценки параметровМеньший . Мы называем коэффициент(Или k) - параметр гребня. Поскольку параметр гребня не уникален, для оценки регрессии гребня мы получаемСобственно параметры регрессииПримерная семья. Например, в следующей таблице:

Карта хребта

. Взаимосвязь между параметрами оценки регрессии и параметром гребенчатой регрессии k в приведенной выше таблице представлена графиком, который является графом трассы гребня.

. Если сингулярности нет, след гребня должен постепенно стремиться к 0.

Когда есть сингулярность, из результата оценки параметров гребневой регрессии можно увидеть, что, когда k недостаточно велик в начале, сингулярность не сильно изменилась, поэтому при изменении k, Оценочные параметры регрессии сильно колеблются: когда k достаточно велико, влияние сингулярности постепенно уменьшается, и значение оцениваемого параметра постепенно становится стабильным.

Общий принцип подбора параметров гребня

Оценка гребня каждого коэффициента регрессии в основном стабильна.
Нет параметров регрессии, явно противоречащих здравому смыслу, и знак оценки гребня должен стать разумным.
Коэффициент регрессии не имеет нереалистичного абсолютного значения.
Остаточная сумма квадратов не сильно увеличивается

Выбрать переменные с гребневой регрессией

Поскольку гребенчатая регрессия является регрессией после стандартизации переменных, размер коэффициентов гребневой регрессии можно сравнивать друг с другом, и стандартизация может быть устранена.
С увеличением k коэффициент регрессии становится нестабильным, и переменную, колебания которой стремятся к нулю, также можно исключить.

Итак, возникает вопрос, как мы можем увидеть тенденцию к 0? Может программа автоматически это определить? Если есть несколько нестабильных коэффициентов регрессии, какой из них следует удалить? Это необходимо определить в соответствии с эффектом регрессии после удаления определенной переменной. Это включает расширенный метод регрессии гребня LASSO.

Перед этим запустите пример регрессии гребня на языке R

Пакет регрессии гребня на языке R - MASS, а функция для выполнения регрессии гребня - lm.ridge

1. Загрузите пакет MASS и используйте в качестве примера встроенный набор данных Longley R (макроэкономические данные). (Примечание: в целом макроэкономические данные будут иметь серьезные проблемы коллинеарности (

Я обнаружил, что результаты нескольких переменных не имеют значения, поэтому следует ли мне удалить эти переменные? Мы используем гребневую регрессию для исключения переменных.

автоматически выбирает параметры регрессии гребня и выдаёт результат

Вопрос, требующий решения: какой цвет представляет какую переменную? . . Нима

. На приведенном выше рисунке вы можете выбрать значение k невооруженным глазом, а затем поместить его в лямбду (лямбда в функции lm.ridge равна 0 на дефолт)

Согласно различным методам выбора k, можно обнаружить, что существует очень большая неопределенность в выборе параметров регрессии гребня.

Тибширани (1996) предложил лассо (наименьшее абсолютное сжатие и

Оператор выбора) алгоритм

В отличие от регрессии гребня, LASSO создает штрафную функцию первого порядка, так что коэффициент некоторых переменных в модели равен 0 (вероятность того, что коэффициент регрессии гребня равен 0, очень высока)
Как и регрессия гребня, LASSO также является необъективной оценкой.

Сравнение моделей

Видно, что штрафная функция LASSO имеет форму абсолютного значения, а ее функциональная форма более сжатая. Более интуитивно понятно объяснять в геометрическом смысле:

На рисунке ниже показано геометрическое представление модели LASSO.

На рисунке ниже показано геометрическое представление гребневой регрессии.

Красный цвет - это область минимального значения, а синий цвет - это область условия ограничения.

Можно обнаружить, что, поскольку LASSO имеет форму абсолютного значения, его ограничения более "четкие". Предполагаемый параметр регрессии, скорее всего, будет равен нулю.

Левая часть изображения выше представляет собой гребневую регрессию, а правая часть - LASSO. Справа налево на каждом рисунке значение k постепенно увеличивается. Видно, что LASSO находится в процессе увеличения значения k,

Параметры регрессии часто оцениваются как 0. Для таких параметров мы можем исключить их. Нам не нужно вручную выбирать для исключения переменные, но мы можем позволить программе автоматически удалять переменные в зависимости от того, равно ли оно 0.

Теперь проблема в том, что, поскольку штрафная функция регрессии LASSO имеет форму абсолютного значения, трудно получить определенное выражение оцениваемых параметров. Как ее решить?

Статистики обнаружили, что результаты вычислений регрессии LASSO и регрессии минимального угла очень похожи, поэтому результаты регрессии минимального угла LAR можно использовать для оценки LASSO. (Конкретные идеи и доказательства очень сложны, и я продолжу писать в блоге, чтобы объяснить это позже).

Использовать набор данных Лонгли

Результат на приведенном выше рисунке является результатом регрессии по методу наименьших квадратов линейной регрессии с использованием алгоритма LAR.

Вы можете видеть, что две переменные Year и Employed многократно удаляются и используются, и эти две переменные должны быть удалены.

В итоговом результате CP представляет оценку коллинеарности. Видно, что модель находится на шаге 8.

Минимальная коллинеарность в сочетании с ситуацией на шаге 8 в laa, поэтому удаление двух переменных Year и Employed означает

Читайте также: