Распределение пуассона с параметром лямбда
Добавил пользователь Morpheus Обновлено: 19.09.2024
Трагедия статистики в большинстве школ заключается в том, насколько она скучна. Учителя часами разбираются в выводах, уравнениях и теоремах, и, когда вы, наконец, доберетесь до самой лучшей части - применяя понятия к реальным числам, - это приводит к не относящимся к делу, невообразимым примерам, таким как бросание кубиков. Это позор, так как статистика может быть приятной, если вы пропустите выводы (которые вам, вероятно, никогда не понадобятся) и сосредоточитесь на использовании идей для решения интересных задач.
В этой статье мы рассмотримПуассоновские процессыиРаспределение Пуассона,две важные вероятностные концепции. Выделив только соответствующую теорию, мы проработаем пример из реальной жизни, показывая уравнения и графики, чтобы представить идеи в правильном контексте.
Пуассоновский процесс - это модель для серии дискретных событий, гдесреднее времяМежду событиями известно, но точное время событий является случайным. Прибытие события не зависит от события до (время ожидания между событиямибез памяти). Например, предположим, что у нас есть веб-сайт, который нашсеть доставки контента (CDN)говорит нам, что происходит сбой в среднем один раз в 60 дней, но один сбой не влияет на вероятность следующего. Все, что мы знаем, это среднее время между отказами. Это пуассоновский процесс, который выглядит следующим образом:

Важным моментом является то, что мы знаемсреднее время между событиямино они расположены случайно (стохастический). У нас могут быть параллельные сбои, но мы также можем годами преодолевать сбои из-за случайности процесса.
Пуассоновский процесссоответствует следующим критериям (в действительности многие явления, смоделированные как пуассоновские процессы, не соответствуют им в точности):
- Событиянезависимыйдруг друга. Возникновение одного события не влияет на вероятность другого события.
- Средняя скорость (события за период времени) постоянна.
- Два события не могут происходить одновременно.
Последний пункт - события не являются одновременными - означает, что мы можем рассматривать каждый подинтервал пуассоновского процесса как процесс Бернулли, то есть либо успех, либо провал. На нашем веб-сайте весь интервал может составлять 600 дней, но каждый дополнительный интервал - один день - наш веб-сайт либо отключается, либо нет.
Типичные примеры пуассоновских процессовклиенты, звонящие в справочный центр, посетители веб-сайта, радиоактивный распад атомов, фотоны, поступающие в космический телескоп, и изменения цены акций. Пуассоновские процессы обычно связаны со временем, но они не должны быть. В случае с запасом мы могли бы знать среднее движение за день (количество событий за время), но у нас также мог бы быть процесс Пуассона для количества деревьев в акре (количество событий на область).
(Одним из примеров, часто приводимых для процесса Пуассона, являются прибытия автобусов (или поезда, или теперь Ubers). Однако это не настоящий процесс Пуассона, поскольку прибытия не зависят друг от друга. Даже для систем шин, которые не работают вовремя, Опоздание одного автобуса влияет на время прибытия следующего автобуса.У Джейка ВандерПласа есть отличная статьяо применении процесса Пуассона ко времени прибытия автобусов, который лучше работает с подготовленными данными, чем с данными реального мира.)
Пуассоновский процессэто модель, которую мы используем для описания случайных событий и сама по себе она не очень полезна. Нам нужноРаспределение Пуассонаделать интересные вещи, такие как нахождение вероятности ряда событий за период времени или нахождение вероятности ожидания некоторого времени до следующего события.
Массовая функция вероятности распределения Пуассона дает вероятность наблюденияКсобытия в период времени с учетом продолжительности периода и среднего события за время:

Это немного запутанно, и период времени / времени * обычно упрощается в один параметр,λ,лямбда, показатель скорости. С помощью этой замены функция вероятности распределения Пуассона теперь имеет один параметр:

Лямбда может рассматриваться какожидаемое количество событий в интервале, (Мы перейдем к названию этого интервала, потому что помните, нам не нужно использовать период времени, мы могли бы использовать площадь или объем на основе нашего процесса Пуассона). Мне нравится выписывать лямбду, чтобы напомнить себе, что параметр скорости является функцией как среднего числа событий за время, так и продолжительности периода времени, но чаще всего вы увидите, что это прямо выше.
Как мы меняем параметр скорости,λмы меняем вероятность увидеть разное количество событий за один интервал Приведенный ниже график представляет собой функцию вероятности массы распределения Пуассона, показывающую вероятность ряда событий, происходящих в интервале с различными параметрами скорости.

Наиболее вероятным числом событий в интервале для каждой кривой являетсяпараметр скорости, Это имеет смысл, потому чтоПараметр скорости - это ожидаемое количество событий в интервалеи поэтому, когда это целое число,параметром скорости будет количество событий с наибольшей вероятностью,
Когда это не целое число, наибольшее число вероятностей событий будет ближайшим целым числом к параметру скорости, поскольку распределение Пуассона определено только для дискретного числа событий. Дискретный характер распределения Пуассона также объясняет, почему этомассафункция, а неплотностьфункция. (Параметр скорости также является средним значением и дисперсией распределения, которые не обязательно должны быть целыми числами.)
Мы можем использовать массовую функцию распределения Пуассона, чтобы найти вероятность наблюдения ряда событий в течение интервала, порожденного пуассоновским процессом. Другое использование уравнения функции массы - как мы увидим позже - это найти вероятность ожидания некоторого времени между событиями.
Для решения проблемы, которую мы решим с помощью дистрибутива Пуассона, мы могли бы продолжить со сбоями веб-сайта, но я предлагаю кое-что более грандиозное. В детстве мой отец часто брал меня во двор, чтобы наблюдать (или пытаться наблюдать)метеоритные дожди, Мы не были космическими фанатами, но наблюдения за объектами из космоса, сгоревшими в небе, было достаточно, чтобы вытащить нас наружу, хотяметеорные потоки всегда казалисьг в самые холодные месяцы.
Количество наблюдаемых метеоров можно смоделировать как распределение Пуассона, поскольку метеоры независимы, среднее число метеоров в час является постоянным (в краткосрочной перспективе), и - это приблизительное значение - метеоры не происходят одновременно. Чтобы охарактеризовать распределение Пуассона, все, что нам нужно, это параметр скорости, который представляет собой число событий / интервал * длина интервала. Из того, что я помню, нам сказалиожидать5 метеоров в часв среднемили1 каждые 12 минут, Из-за ограниченного терпения маленького ребенка (особенно в морозную ночь) мы никогда не задерживались более 60 минут, поэтому мы будем использовать это в качестве периода времени. Соединяя их вместе, мы получаем:


14% или около 1/7. Если бы мы выходили на улицу каждую ночь в течение одной недели, то могли ожидать, что мой папа будет прав ровно один раз! Хотя приятно знать, что мы ищем распределение, вероятность увидеть разное количество метеоров. Делать это вручную утомительно, поэтому мы будем использовать Python -который вы можете увидеть в этом ноутбуке Jupyter- для расчета и визуализации.
На приведенном ниже графике показана функция вероятности массы для числа метеоров в часе со средним временем между метеорами 12 минут (что аналогично тому, как говорят, что 5 метеоров ожидаются в часе).

Мы уже подсчитали, что вероятность увидеть ровно 3 метеора составляет около 14%. Шанс увидеть3 или меньше метеоровза один час составляет 27%, что означает вероятность увидетьболее 3составляет 73%. Аналогичным образом, вероятность более 5 метеоров составляет 38,4%, в то время как мы можем ожидать увидеть 5 или менее метеоров в 61,6% часов наблюдений. Несмотря на то, что он небольшой, с вероятностью 1,4% можно наблюдать более 10 метеоров в час!
Чтобы визуализировать эти возможные сценарии, мы можем провести эксперимент, попросив нашу сестру записать количество метеоров, которые она видит каждый час в течение 10 000 часов. Результаты показаны на гистограмме ниже:

(Это, очевидно, симуляция. Для этой статьи не было ни одной сестры.) Глядя на возможные результаты, можно утверждать, что этораспределениеи ожидаемый результат не всегда происходит. В несколько счастливых ночей мы видели 10 или более метеоров в час, хотя обычно мы видели 4 или 5 метеоров.
Экспериментируя с параметром скорости
Параметр скорости,λ,это единственное число, которое нам нужно для определения распределения Пуассона. Однако, поскольку он является произведением двух частей (события / интервал * длина интервала), есть два способа его изменить: мы можем увеличивать или уменьшать события / интервал и мы можем увеличивать или уменьшать длину интервала.
Во-первых, давайте изменим параметр скорости, увеличив или уменьшив количество метеоров в час, чтобы увидеть, как это влияет на распределение. Для этого графика мы поддерживаем постоянный период времени равным 60 минутам (1 час).

В каждом случае наиболее вероятное число метеоров в течение часа - это ожидаемое количество метеоров, параметр скорости для распределения Пуассона. Например, при скорости 12 метеоров в час (миль в час) наш показатель скорости равен 12, и есть вероятность 11% наблюдать ровно 12 метеоров за 1 час. Если наш показатель скорости увеличивается, мы должны ожидать больше метеоров в час.
Другой вариант - увеличить или уменьшить длину интервала. Ниже показан тот же график, но на этот раз мы сохраняем число метеоров в час постоянным на уровне 5 и меняем продолжительность наблюдаемого нами времени.

Интригующая часть пуассоновского процесса включает в себя выяснение того, как долго мы должны ждать следующего события (это иногда называют временем взаимодействия). Рассмотрим ситуацию: метеоры появляются в среднем каждые 12 минут. Если мы прибудем в случайное время, как долго мы можем ожидать, чтобы увидеть следующий метеор? Мой папа всегда (на этот раз с оптимизмом) утверждал, что нам нужно было ждать только 6 минут до первого метеора, который согласуется с нашей интуицией. Однако еслимы узнали что-нибудьдело в том, что наша интуиция не годится для вероятности.
Я не буду вдаваться в вывод (он исходит из уравнения функции вероятности), но время, которое мы можем ожидать между событиями, является экспоненциальной затухающей. Вероятность ожидания определенного промежутка времени между последовательными событиями уменьшается экспоненциально с увеличением времени. Следующее уравнение показывает вероятность ожидания больше указанного времени.

В нашем примере у нас есть 1 событие / 12 минут, и если мы подключим числа, мы получим 60,65% шансов на ожидание> 6 минут. Так много для предположения моего отца! Чтобы показать другой случай, мы можем ожидать более 30 минут, примерно 8,2% времени. (Следует отметить, что это происходит между каждой последовательной парой событий. Время ожидания между событиями не имеет памяти, поэтому время между двумя событиями не влияет на время между любыми другими событиями. Это отсутствие памяти также известно какМарковская недвижимость).
График помогает нам визуализировать экспоненциальный спад времени ожидания:
Существует 100% вероятность ожидания более 0 минут, что составляет почти 0% вероятности ожидания более 80 минут. Опять же, поскольку это распределение, существует широкий диапазон возможных интервалов взаимодействия.
И наоборот, мы можем использовать это уравнение, чтобы найти вероятность ожидания меньше или равна времени:
Мы можем ожидать 6 минут или меньше, чтобы увидеть метеор в 39,4% случаев. Мы также можем найти вероятность ожидания определенного периода времени: существует вероятность 57,72% ожидания от 5 до 30 минут, чтобы увидеть следующий метеор.
Чтобы визуализировать распределение времени ожидания, мы можем еще раз запустить (смоделированный) эксперимент. Мы моделируем наблюдение в течение 100 000 минут со средней скоростью 1 метеор / 12 минут. Затем мы находим время ожидания между каждым видимым метеором и строим график распределения.
Наиболее вероятное время ожидания составляет 1 минуту, но это несреднее время ожидания.Давайте вернемся к первоначальному вопросу: сколько времени мы можем ожидать в среднем, чтобы увидеть первый метеор, если мы прибудем в случайное время?
Чтобы ответить на вопрос о среднем времени ожидания, мы проведем 10 000 отдельных испытаний, каждый раз наблюдая за небом в течение 100 000 минут. На графике ниже показано распределение среднего времени ожидания между метеорами из этих испытаний:

Среднее из 10000 средних составляет 12,003 минуты. Даже если мы прибудем в случайное время,среднее время ожидания первого метеора - это среднее время между событиями.Во-первых, это может быть трудно понять: если события происходят в среднем каждые 12 минут, то почему мы должны ждать целых 12 минут, чтобы увидеть одно событие? Ответ: это среднее время ожидания с учетом всех возможных ситуаций.
Если метеоры приходили ровно каждые 12 минут, то в среднем мы должны ждать, чтобы увидетьпервыйбудет 6 минут. Однако, поскольку это экспоненциальное распределение, иногда мы обнаруживаемся и вынуждены ждать час, что перевешивает большее количество раз, когда мы ждем менее 12 минут. Это называетсяОжидание парадокса времени и стоит прочитать.
В качестве окончательной визуализации давайте проведем случайную симуляцию продолжительностью 1 час наблюдения.

Ну, на этот раз мы получили именно то, что ожидали: 5 метеоров. Мы должны были ждать 15 минут для первого, но затем были хорошие падающие звезды. По крайней мере, в этом случае стоило бы выйти из дома для небесного наблюдения!
Заметки о распределении Пуассона и биномиальном распределении
Биномиальное распределение используется для моделирования вероятности числа успехов, которые мы можем ожидать от n испытаний с вероятностью p. Распределение Пуассона является частным случаем биномиального распределения, так как n стремится к бесконечности, в то время как ожидаемое число успехов остается фиксированным. Пуассон используется в качестве аппроксимации бинома, если n велико, а p мало.
Заметки о метеорах / метеоритах / метеоритах / астероидах
Метеоритыэто полосы света, которые вы видите на небе, которые вызваны кусками мусора, называемыми метеоритами, сгорающими в атмосфере.метеорное теломожет исходить от астероида, кометы или кусочка планеты и обычно имеет диаметр в миллиметрах, но может достигать километра. Если метеороид переживает свое путешествие через атмосферу и воздействует на Землю, он называетсяметеорит,Астероидынамного большие куски скалы, вращающиеся вокруг солнца в поясе астероидов. Разрушающиеся части астероидов становятся метеороидами.Чем больше ты знаешь!.
Выводы
Подводя итог, можно сказать, что распределение Пуассона дает вероятность ряда событий в интервале, порожденном пуассоновским процессом. Распределение Пуассона определяется параметром скорости,λ, которое представляет собой ожидаемое количество событий в интервале (события / интервал * длина интервала) и наибольшее число вероятностей событий. Мы также можем использоватьРаспределение Пуассона, чтобы найти время ожиданиямежду событиями. Даже если мы прибудем в случайное время, среднее время ожидания всегда будет средним временем между событиями.
В следующий раз, когда вы потеряете фокус в статистике, у вас будет мое разрешение перестать обращать внимание на учителя. Вместо этого найдите соответствующие уравнения и примените их к интересной задаче. Вы можете изучить материал и оценить, как статистика помогает нам понять мир. Прежде всего, оставайтесь любопытными: в мире есть много удивительных явлений, и мы можем использовать науку о данных - отличный инструмент для их изучения,
Как всегда, я приветствую отзывы и конструктивную критику. Со мной можно связаться в твиттере@koehrsen_will.
Задача до боли эйфории знакома:
– проводится независимых испытаний, в каждом из которых случайное событие может появиться с вероятностью. Требуется найти вероятность того, что в данной серии испытаний событие появится ровно раз.
Наверное, вам уже снится формула Бернулли:)
тем более, на уроке о биномиальном распределении вероятностей мы разобрали ситуацию по косточкам.
В том случае, если количество испытаний велико (сотни и тысячи), эту вероятность обычно рассчитывают приближённо – с помощью локальной теоремы Лапласа: , где .
Итак, если количество испытаний достаточно велико, а вероятность появления события в отдельно взятом испытании весьма мала (0,05-0,1 и меньше), то вероятность того, что в данной серии испытаний событие появится ровно раз, можно приближенно вычислить по формуле Пуассона:
, где
Напоминаю, что ноль факториал , а значит, формула имеет смысл и для .
В новом микрорайоне поставлено 10000 кодовых замков на входных дверях домов. Вероятность выхода из строя одного замка в течение месяца равна 0,0002. Найти вероятность того, что за месяц откажет ровно 1 замок.
Утопичная, конечно, задача, но что делать – решаем:)
Вычислим:
– по существу, это среднеожидаемое количество вышедших из строя замков.
Таким образом:
– вероятность того, что за месяц из строя выйдет ровно один замок (из 10 тысяч).
Ответ:
С технической точки зрения этот результат можно получить несколькими способами, расскажу о них в историческом ракурсе:
1) С помощью специальной таблицы, которая до сих пор встречается во многих книгах по терверу. В данную таблицу сведены различные значения и соответствующие им вероятности. Табулирование обусловлено тем, что в своё время не существовало бытовых калькуляторов, на которых можно было бы подсчитать значения экспоненциальной функции. Отсюда, кстати, идёт традиция округлять вычисления до 4 знаков после запятой – как в стандартной таблице.
2) С помощью прямого вычисления на микрокалькуляторе (прогресс!).
3) С помощью стандартной экселевской функции:
=ПУАССОН(m; лямбда; 0)
в данной задаче вбиваем в любую ячейку Экселя =ПУАССОН(1; 2; 0) и жмём Enter.
Следует отметить, что развитие вычислительной техники фактически отправило в историю методы Лапласа, да и рассматриваемый метод тоже – по той причине, что ответ легко вычислить более точно по формуле Бернулли:
Здесь я использовал функцию БИНОМРАСП, о которой неоднократно упоминал ранее.
Но формула Пуассона, тем не менее, даёт очень крутое приближение:
– с погрешностью только на 9 знаке после запятой!
Впрочем, это всё лирика, решать-то всё равно нужно по формуле Пуассона:
Завод отправил в торговую сеть 500 изделий. Вероятность повреждения изделия в пути равна 0,003. Найти вероятность того, что при транспортировке будет повреждено: а) ни одного изделия, б) ровно три изделия, в) более трех изделий.
Решение: используем формулу Пуассона:
В данном случае:
– среднеожидаемое количество повреждённых изделий
а)
– вероятность того, что все изделия дойдут в целости и сохранности. Ничего не украдут, одним словом :)
б)
– вероятность того, что в пути будут повреждены ровно 3 изделия из 500.
в)
А тут всё немножко хитрее. Сначала найдём – вероятность того, что в пути повредятся не более трёх изделий. По теореме сложения вероятностей несовместных событий:
Само собой, ручками это считать надоест, и поэтому я добавил в свой расчётный макет автоматическое построение распределения Пуассона (см. Пункт 7) – пользуйтесь на здоровье.
По теореме сложения вероятностей противоположных событий:
– вероятность того, что при доставке будет повреждено более 3 изделий.
Ответ: а) , б) , в)
Вероятность изготовления бракованных деталей при их массовом производстве равна . Определить вероятность того, что в партии из 800 деталей будет: а) ровно 2 бракованные, б) не более двух.
Решение и ответ в конце урока.
В этой связи ни в коем случае не отключаем голову – даже в таких простых примерах!
А теперь о самом распределении Пуассона. Случайная величина , распределённая по этому закону, принимает бесконечное и счётное количество значений , вероятности появления которых определяются формулой:

Или, если расписать подробно:
Вспоминая разложение экспоненты в ряд, легко убедиться, что:
В теории установлено, что математическое ожидание пуассоновской случайной величины равно и дисперсия – тому же самому значению: .
Обратите внимание, что во всех вышеприведённых заданиях мы лишь ПОЛЬЗОВАЛИСЬ распределением Пуассона для приближенного расчёта вероятностей, в то время как ТОЧНЫЕ значения следовало находить по формуле Бернулли, т.е., там имело место биномиальное распределение.
И следующие две задачи принципиально отличаются от предыдущих:
Случайная величина подчинена закону Пуассона с математическим ожиданием . Найти вероятность того, что данная случайная величина примет значение, меньшее, чем ее математическое ожидание.
Отличие состоит в том, что здесь речь идёт ИМЕННО о распределении Пуассона.
Решение: случайная величина принимает значения с вероятностями:
По условию, , и тут всё просто: событие состоит в трёх несовместных исходах:
вероятность того, что случайная величина примет значение, меньшее, чем ее математическое ожидание.
Ответ:
Аналогичная задача на понимание:
Случайная величина подчинена закону Пуассона с математическим ожиданием . Найти вероятность того, что данная случайная величина примет положительное значение.
Решение и ответ в конце урока.
Помимо приближения биномиального распределения (Примеры 1-3), распределение Пуассона нашло широкое применение в теории массового обслуживания для вероятностной характеристики простейшего потока событий. Постараюсь быть лаконичным:
Итак, пусть в некоторую систему поступает простейший поток заявок со средней интенсивностью заявок в некоторую единицу времени (минуту, час, день или в любую другую). Тогда вероятность того, что за данный промежуток времени, в систему поступит ровно заявок, равна:
Звонки в диспетчерскую такси представляет собой простейший пуассоновский поток со средней интенсивностью 30 вызовов в час. Найти вероятность того, что: а) за 1 мин. поступит 2-3 вызова, б) в течение пяти минут будет хотя бы один звонок.
Решение: используем формулу Пуассона:
а) Учитывая стационарность потока, вычислим среднее количество вызовов за 1 минуту:
вызова – в среднем за одну минуту.
По теореме сложения вероятностей несовместных событий:
– вероятность того, что за 1 минуту в диспетчерскую поступит 2-3 вызова.
б) Вычислим среднее количество вызов за пять минут:
По формуле Пуассона:
– вероятность того, что в течение 5 минут не будет ни одного звонка.
По теореме сложения вероятностей противоположных событий:
– вероятность того, что в течение 5 минут будет хотя бы один вызов.
Ответ: а) , б)
Заметьте, что, несмотря на конечное количество возможных звонков (а оно в принципе конечно), здесь имеет место именно распределение Пуассона, а не какое-то другое.
Для самостоятельного решения:
Среднее число автомобилей, проходящих таможенный досмотр в течение часа, равно 3. Найти вероятность того, что: а) за 2 часа пройдут досмотр от 7 до 10 автомобилей; б) за полчаса успеет пройти досмотр только 1 автомобиль.
Решение и ответ в конце урока.
Наверное, многие знают, что теория массового обслуживания – это обширный и очень интересный раздел прикладной математики, и сейчас мы познакомились с простейшей его задачей.
Дополнительные примеры на распределение и формулу Пуассона можно найти в тематической pdf-книге, и я предлагаю вам ознакомиться с ещё одной популярной вещью – Гипергеометрическим распределением вероятностей.
Приятного и полезного чтения!
Решения и ответы:
Пример 3. Решение: используем формулу Пуассона:
, в данном случае:
а) – вероятность того, что в данной партии окажется ровно 2 бракованные детали.
б) По теореме сложения вероятностей несовместных событий:
– вероятность того, что в данной партии окажется не более 2 бракованных изделий.
Пример 5. Решение: случайная величина принимает значения с вероятностями . По условию, .
Найдём вероятность того, что случайная величина примет нулевое значение:
По теореме сложения вероятностей противоположных событий:
– вероятность того, что случайная величина примет положительное значение
Пример 7. Решение: предполагая поток простым, используем формулу Пуассона:
а) Вычислим – среднее количество автомобилей, проходящих таможенный досмотр, в течение 2 часов.
По теореме сложения вероятностей несовместных событий:
– вероятность того, что за 2 часа досмотр пройдут от 7 до 10 автомобилей
б) Вычислим – среднее количество автомобилей, проходящих досмотр, за 1/2 часа.
По формуле Пуассона:
– вероятность того, что за полчаса таможенный досмотр пройдёт только один автомобиль.
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Закон Пуассона , где λ равна среднему числу появления событий в одинаковых независимых испытаниях, т.е. λ = n × p, где p – вероятность события при одном испытании, e = 2,71828 .
В случае, когда n велико, а λ = p·n > 10 формула Пуассона дает очень грубое приближение и для расчета Pn(m) используют локальную и интегральную теоремы Муавра-Лапласа.
Числовые характеристики случайной величины Х
Дисперсия распределения Пуассона
D[X] = λ
Пример №1 . Семена содержат 0.1% сорняков. Какова вероятность при случайном отборе 2000 семян обнаружить 5 семян сорняков?
Решение.
Вероятность р мала, а число n велико. np = 2 5 e -5 /5! = 0.03609
Математическое ожидание: M[X] = λ = 2
Дисперсия: D[X] = λ = 2
Пример №2 . Среди семян ржи имеется 0.4% семян сорняков. Составить закон распределения числа сорняков при случайном отборе 5000 семян. Найти математическое ожидание и дисперсию этой случайной величины.
Решение. Математическое ожидание: M[X] = λ = 0.004*5000 = 20. Дисперсия: D[X] = λ = 20
Закон распределения:
| X | 0 | 1 | 2 | … | m | … |
| P | e -20 | 20e -20 | 200e -20 | … | 20 m e -20 /m! | … |
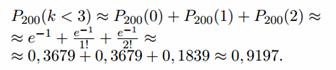
Пример №3 . На телефонной станции неправильное соединение происходит с вероятностью 1/200. Найдите вероятность того, что среди 200 соединений произойдет:
а) ровно одно неправильное соединение;
б) меньше чем три неправильных соединения;
в) больше чем два неправильных соединения.
Решение. По условию задачи вероятность события мала, поэтому используем формулу Пуассона (15).
а) Задано: n = 200, p = 1/200, k = 1. Найдем P200(1).
Получаем: . Тогда P200(1) ≈ e -1 ≈ 0,3679.
б) Задано: n = 200, p = 1/200, k < 3. Найдем P200(k < 3).
Имеем: a = 1.
в) Задано: n = 200, p = 1/200, k > 2. Найдем P200(k > 2).
Эту задачу можно решить проще: найти вероятность противоположного события, так как в этом случае нужно вычислить меньше слагаемых. Принимая во внимание предыдущий случай, имеем
P200(k>2) = 1-P200(k≤2) = 1-P200(k n является достаточно большим, а p — достаточно малым; положим np = a , где a — некоторое число. В этом случае искомая вероятность определяется формулой Пуассона:
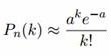
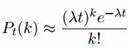
где λ — интенсивность потока событий, то есть среднее число событий, которые появляются в единицу времени.
Пример №4 . Вероятность того, что деталь бракованная, равна 0.005. проверяется 400 деталей. Укажите формулу вычисления вероятности того, что больше 3 деталей оказались с браком.
Пример №5 . Вероятность появления бракованных деталей при их массовом производстве равна p. определить вероятность того, что в партии из N деталей содержится а) ровно три детали; б) не более трех бракованных деталей.
p=0,001; N = 4500
Решение.
Вероятность р мала, а число n велико. np = 4.5 < 10. Значит случайная величина Х – распределена по Пуассоновскому распределению. Составим закон.
Случайная величина X имеет область значений (0,1,2. m). Вероятности этих значений можно найти по формуле:
Найдем ряд распределения X.
Здесь λ = np = 4500*0.001 = 4.5
P(0) = e - λ = e -4.5 = 0.01111
P(1) = λe -λ = 4.5e -4.5 = 0.04999
Тогда вероятность того, что в партии из N деталей содержится ровно три детали, равна:
Тогда вероятность того, что в партии из N деталей содержится не более трех бракованных деталей:
P(x<3) = P(0) + P(1) + P(2) = 0,01111 + 0,04999 + 0,1125 = 0,1736
Пример №6 . Автоматическая телефонная станция получает в среднем за час N вызовов. Определить вероятность того, что за данную минуту она получит: а) ровно два вызова; б) более двух вызовов.
N = 18
Решение.
За одну минуту АТС в среднем получает λ = 18/60 мин. = 0,3
Считая, что случайное число X вызовов, поступивших на АТС за одну минуту,
подчиняется закону Пуассона, по формуле найдем искомую вероятность
Найдем ряд распределения X.
Здесь λ = 0.3
P(0) = e - λ = e -0.3 = 0.7408
P(1) = λe -λ = 0.3e -0.3 = 0.2222
Вероятность того, что за данную минуту она получит ровно два вызова:
P(2) = 0,03334
Вероятность того, что за данную минуту она получит более двух вызовов:
P(x>2) = 1 – 0,7408 – 0,2222 – 0,03334 = 0,00366
Пример №7 . Рассматриваются два элемента, работающих независимо друг от друга. Продолжительность времени безотказной работы имеет показательное распределение с параметром λ1 = 0,02 для первого элемента и λ2 = 0,05 для второго элемента. Найти вероятность того, что за 10 часов: а) оба элемента будут работать безотказно; б) только Вероятность того, что за 10 часов элемент №1 не выйдет из строя:
Рещение.
P1(0) = e -λ1*t = e -0.02*10 = 0,8187
Вероятность того, что за 10 часов элемент №2 не выйдет из строя:
P2(0) = e -λ2*t = e -0.05*10 = 0,6065
а) оба элемента будут работать безотказно;
P(2) = P1(0)*P2(0) = 0,8187*0,6065 = 0,4966
б) только один элемент выйдет из строя.
P(1) = P1(0)*(1-P2(0)) + (1-P1(0))*P2(0) = 0.8187*(1-0.6065) + (1-0.8187)*0.6065 = 0.4321
Пример №7 . Производство даёт 1% брака. Какова вероятность того, что из взятых на исследование 1100 изделий выбраковано будет не больше 17?
Примечание: поскольку здесь n*p =1100*0.01=11 > 10, то необходимо использовать теорему Лапласа.
Если у Вашего провайдера происходят обрывы в среднем на 20 минут в неделю, то какова вероятность, что сегодня интернета не будет целый час? 22.3%! А вот на два часа мы останемся без интернета с вероятностью только 4.3%. Итак, распределение Пуассона как раз для этого, зная среднее значение, мы можем получить вероятность, что событие произойдёт за интересующий нас период.
Вероятность (в общем)
Очень важная вероятность, используется буквально ежедневно на производстве и в сфере обслуживания и других науках. Суть очень проста: если мы знаем вероятность события и если такие события происходят независимо друг от друга, то мы можем узнать:
- a. Вероятность, что произойдёт N событий
- b. Вероятность, что произойдёт меньше или больше чем N событий
Вероятность (конкретный случай)
Пример
На заводе производят 1000 метров кабеля в день, стоимостью 500 рублей за 1 м. В среднем обнаруживается один брак на 300 метров произведённого и тогда метр провода обрезается. Какова вероятность, что за три дня завод потеряет больше 7000 рублей?
Вероятность, что провод окажется бракованным равна 1/300 ~ 0.0033.
Потери завода на 7000 рублей - это 14 бракованных метров.
Параметр лямбда для трёх дней равен: λ 3000*0.0033 = 10.
Куммулятивное значение распределения Пуассона для λ = 10 равно F(14) = 0.9165, откуда вероятность получить больше 14 бракованных метров за три дня равна 1-0.9165 = 0.08835 = 8.3%.
Распределение Пуассона - определение
Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Другими словами, если событие происходит с некоторой периодичностью, то мы можем определить вероятность, что такое событие произойдёт n раз за интересующий нас период.
Параметр лямбда - λ
Распределение Пуассона зависит только от одного параметра - λ, данный параметр зависит от вероятности успешного события и общего количества событий.
Успешное событие: распределение Пуассона применяется только тогда, когда есть разделение на результат "да" и "нет", например, лампочка перегорела: да - успешное событие; шина прокололась: да - успешное событие и так далее.
λ = n*p, где p - вероятность успешного события, а n - общее количество событий, для которых ведётся расчёт.
Например, если гроза проходит раз в месяц и мы хотим посчитать вероятность грозы за 24 месяца, то вероятность равна единице, а количество событий равно 24, откуда лямбда равна 24.
Можно считать по-другому, вероятность грозы в конкретный день - 1/30, количество событий - 730 дней, лямбда равна 24.3.
Пример
В тысяче ящиков с антоновками в одном попадается голден, какова вероятность, что в 5000 ящиках будет меньше 4 ящиков с яблоком голден?
Вероятность ящика с яблоком голден - 0.1% (1 ящик на 1000 = 1/1000, если в процентах - 1/1000 * 100 = 0.1%)
Общее количество событий - 5000 ящиков
Из вышесказанного следует:
λ = 5000 * 0.001 = 5
Откуда вероятность равна 26.5% (калькулятор ниже).
Функция вероятности (формула Пуассона)
Вероятность, что успешное событие произойдёт k раз:
Пример
В тысяче ящиков с антоновками в одном попадается голден, какова вероятность, что в 5000 ящиках будет 2 ящика с яблоком голден?
Из предыдущего примера мы знаем, что λ=5, теперь мы ищем вероятность, что k будет равно 2, для этого используем формулу функции вероятности:
Закон распределения
График распределения Пуассона
Обратите внимание, что при увеличении λ, график распределения становится похож на график нормального распределения.
Распределение Пуассона: формула вероятности редких событий
Распределение Пуассона - случай биномиального распределения, когда число испытаний n достаточно большое, а вероятность p события A мала ().
Распределение Пуассона называют также распределением редких событий. Например, рождение за год трёх или четырёх близнецов, тот же закон распределения имеет число распавшихся в единицу времени атомов радиоактивного вещества и др.
Вероятность наступления редких событий вычисляется по формуле Пуассона:
где m число наступления события A;
- среднее значение распределения Пуассона;
e=2,7183 - основание натурального логарифма.
Закон Пуассона зависит от одного параметра - λ (лямбда), смысл которого в следующем: он является одновременно математическим ожиданием и дисперсией случаной величины, распределённой по закону Пуассона.
Условия возникновения распределения Пуассона
Рассмотрим условия, при которых возникает распределение Пуассона.
Во-первых, распределение Пуассона является предельным для биномиального распределения, когда число опытов n неограниченно увеличивается (стремится к бесконечности) и одновременно вероятность p успеха в одном опыте неограниченно уменьшается (стремится к нулю), но так, что их произведение np сохраняется в пределе постоянным и равным λ (лямбде):
В математическом анализе доказано, что распределение Пуассона с параметром λ = np можно приближенно применять вместо биномиального, когда число опытов n очень велико, а вероятность p очень мала, то есть в каждом отдельном опыте событие A появляется крайне редко.
Во-вторых, распределение Пуассона имеет место, когда есть поток событий, называемым простейшим (или стационарным пуассоновским потоком). Потоком событий называют последовательность таких моментов, как поступление вызовов на коммуникационный узел, приходы посетителей в магазин, прибытие составов на сортировочную горку и тому подобных. Пуассоновский поток обладает следующими свойствами:
- стационарность: вероятность наступления m событий в определённый период времени постоянна и не зависит от начала отсчёта времени, а зависит только от длины участка времени;
- ординарность: вероятность попадания на малый участок времени двух или более событий пренебрежимо мала по сравнению с вероятностью попадания на него одного события;
- отсутствие последствия: вероятность наступления m событий в определённый период времени не зависит от того, сколько событий наступило в предыдущий период.
Характеристики случайной величины, распределённой по закону Пуассона
Характеристики случайной величины, распределённой по закону Пуассона:
Распределение Пуассона и расчёты в MS Excel
Вероятность распределения Пуассона P(m) и значения интегральной функции F(m) можно вычислить при помощи функции MS Excel ПУАССОН.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши).

MS Excel требует ввести следующие данные:
- x - число событий m;
- среднее;
- интегральная - логическое значение: 0 - если нужно вычислить вероятность P(m) и 1 - если вероятность F(m).
Решение примеров с распределением Пуассона
Пример 1. Менеджер телекоммуникационной компании решил рассчитать вероятность того, что в некотором небольшом городе в течении пяти минут поступят 0, 1, 2, . вызовов. Выбраны случайные интервалы в пять минут, подсчитано число вызовов в каждый их интервалов и рассчитано среднее число вызовов: .
Вычислить вероятность того, что в течении пяти минут поступят 6 вызовов.
Решение. По формуле Пуассона получаем:
Тот же результат получим, используя функцию MS Excel ПУАССОН.РАСП (значение интегральной величины - 0):
Вычислим вероятность того, что в течение пяти минут поступят не более 6 вызовов (значение интегральной величины - 1):
Решить пример самостоятельно, а затем посмотреть решение
Пример 2. Производитель отправил в некоторый город 1000 проверенных, то есть исправных телевизоров. Вероятность того, что при транспортировке телевизор выйдет из строя, равна 0,003. То есть в этом случае действует закон распределения Пуассона. Найти вероятность того, что из всех доставленных телевизоров неисправными будут: 1) два телевизора; 2) менее двух телевизоров.
Продолжаем решать примеры вместе
Пример 3. В центр звонков клиентов поступает поток звонков с интенсивностью 0,8 звонков в минуту. Найти вероятность того, что за 2 минуты: а) не придёт ни одного звонка; б) придёт ровно один звонок; в) придёт хотя бы один звонок.
Решение. Случайная величина X - число звонков за 2 минуты с параметром - распределена по закону Пуассона. У нас есть всё, чтобы вычислить требуемые в условии задачи вероятности:
Пример 4. Поток грузовых железнодорожных составов, прибывающих на сортировочную горку, имеет интенсивность 4 состава в час. Найти вероятности того, что за полчаса на горку прибудет: а) ровно один состав; б) хотя бы один состав; в) не менее трёх составов.
Решение. Случайная величина X - число составов за 0,5 часа с параметром - распределена по закону Пуассона. Вычисляем требуемые в условии задачи вероятности:
Читайте также:

