Лямбда критическая что это

Добавил пользователь Валентин П.
Обновлено: 07.08.2024

Как уже говорилось ранее, в чистом бестиповом лямбда-исчислении отсутствует всё, кроме функций. Так что даже такие элементарные вещи, как числа или булевы значения необходимо реализовывать самим. Точнее, надо создать некие активные сущности, которые будут вести себя подобно необходимым нам объектам. И, естественно, процесс кодирования будет заключаться в написании соответствующих функций.

Начнём мы с самого простого: True и False . Два терма, воплощающие поведение этих констант, выглядят следующим образом:

tru = λt.λf.t	Двухаргументная функция, всегда возвращающая первый аргумент
fls = λt.λf.f	Двухаргументная функция, всегда возвращающая второй аргумент

Оператор if под такие булевы константы будет имеет вид:
if = λb. λx. λy.b x y
Здесь b — tru или fls , x — ветка then , y — ветка else .

Посмотрим, как это будет работать:
if fls t e

Поскольку условие if ложно ( fls ), то должно возвращаться выражение из ветки else ( e в нашем случае).

(λb. λx. λy. b x y) fls t e	по определению if
(λx. λy. fls x y) t e	редукция подчёркнутого выражения из предыдущей строки
(λy. fls t y) e	редукция подчёркнутого выражения из предыдущей строки
fls t e	редукция подчёркнутого выражения из предыдущей строки
(λt.λf. f) t e	по определению fls
(λf. f) e	редукция подчёркнутого выражения из предыдущей строки
e	редукция подчёркнутого выражения из предыдущей строки

or = λx.λy. x tru y

not = λx. x fls tru

Числа Чёрча

Мы с вами будем кодировать только натуральные числа, для чего вспомним аксиомы Пеано, определяющие их множество. В основе реализации по-прежнему будут лежать функции, ведущие себя в заданном контексте подобно единице, двойке и т.д. Собственно, это одна из особенностей лямбда-исчисления: сущности, записанные в его терминах, не обладают самодостаточностью, поскольку воплощают поведение того или иного объекта.

Итак, нам нужна функция, принимающая два аргумента: фиксированное начальное значение и функцию для определения следующего элемента (функцию следования). Число будет закодировано в количестве применений функции следования к начальному значению:

0 ≡ λs.λz. z	функция s применяется к начальному значению z нуль раз
1 ≡ λs.λz. s z	функция s применяется к начальному значению z один раз
2 ≡ λs.λz. s (s z)	функция s применяется к начальному значению z два раза
.	и так далее

Легко заметить, что нуль кодируется так же, как и логическое False. Тем не менее, не стоит делать из этого какие-либо далеко идущие выводы: это всего лишь совпадение.

Задача функции следования состоит в том, чтобы прибавить к заданному числу единицу. Т.е. в качестве аргумента она будет принимать значение, которое требуется увеличить, и которое тоже является функцией двух аргументов. Таким образом, суммарно функция (+1) имеет три аргумента: предшествующее число Чёрча n , функцию, которую надо будет применить n+1 раз к начальному значению, и само начальное значение. Выглядит это так:
scc = λn. λs. λz. s (n s z)
Здесь n s z — n раз применённая к z функция s . Но нам нужно применить её n+1 раз, откуда и берётся явное s (n s z) .

Арифметические операции

Сложение

Функция, осуществляющая сложение двух чисел Чёрча, будет принимать два слагаемых: x и y , которые в свою очередь тоже имеют по два аргумента — s (функцию следования) и z (начальное значение). Сложение будет состоять в том, чтобы сначала применить s к z x раз, а потом ещё y раз.

plus = λx. λy. λs. λz. x s (y s z)

В качестве примера сложим one = λs.λz. s z и two = λs.λz. s (s z) . Ответ должен будет выглядеть так: three = λs.λz. s (s (s z)) .

plus one two s' z'	s' и z' — чтобы не путать подставляемые значения с именами переменных
(λx. λy. λs. λz. x s (y s z)) one two s' z'	по определению plus
one s' (two s' z')	после проведения редукции
(λs.λz. s z) s' (two s' z')	по определению one
s' (two s' z')	после проведения редукции
s' (( λs.λz. s (s z) s' z')	по определению two
s' (s' (s' z'))	после проведения редукции
three s' z'	по определению three

Умножение

Функцию для умножения можно определить через функцию сложения. В конце-концов, умножить x на y означает сложить x копий y .

times = λx. λy. x (plus y) z

Есть ещё один способ определения умножения на числах Чёрча, без использования plus . Его идея заключается в том, что для получения произведения x и y нужно x раз взять y раз применённую к начальному значению функцию s :

times' = λx.λy.λs.λz. x (y s) z

Для примера умножим two = λs.λz. s (s z) на three = λs.λz. s (s (s z)) . Результат должен будет иметь вид: six = λs.λz. s (s (s (s (s (s z))))) .

times' two three s' z'	s' и z' — чтобы не путать подставляемые значения с именами переменных
(λx.λy.λs.λz. x (y s) z) two three s' z'	по определению times'
two (three s') z'	после проведения редукции
(λs.λz. s (s z)) (three s') z'	по определению two
three s' ((three s') z')	после проведения редукции
(λs.λz. s (s (s z))) s' ((three s') z')	по определению three
s' (s' (s' ((three s') z')))	после проведения редукции
s' (s' (s' (((λs.λz. s (s (s z))) s') z')))	по определению three
s' (s' (s' (( (λz. s' (s' (s' z))) z' )))	после проведения редукции
s' (s' (s' (s' (s' (s' z')))))	редукция подчёркнутого выражения
six s' z'	по определению six

Определите терм для возведения числа в степень

Для x в степени y :

power = λx.λy.λs.λz . y x s z

Заключение

Как видим, технически ничего сложного в лямбда-исчислении нет: всё сводится к элементарным подстановкам и редукциям. Но столь малого набора инструментов вполне хватает, чтобы при желании реализовать активные сущности, ведущие себя подобно парам, спискам, рекурсивным функциям и т.п. Они будут достаточно громоздкими, но, как уже говорилось, λ-исчисление предназначено не для написания программ, а для исследования и спецификации языков программирования и систем типов. С чем, собственно, и прекрасно справляется.

Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.

Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…

λ-исчисление: основные понятия

Синтаксис

В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, ~~только хардкор~~. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.

Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.

Термы:

переменная:	x
лямбда-абстракция (анонимная функция):	λx.t , где x — аргумент функции, t — её тело.
применение функции (аппликация):	f x , где f — функция, x — подставляемое в неё значение аргумента

Применение функции левоассоциативно. Т.е. s t u — это тоже самое, что (s t) u
Аппликация (применение или вызов функции по отношению к заданному значению) забирает себе всё, до чего дотянется. Т.е. λx. λy. x y x означает то же самое, что λx. (λy. ((x y) x))
Скобки явно указывают группировку действий.

Процесс вычисления

Рассмотрим следующий терм-применение:

Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:

который для простоты можно переписать как

(напомним, что id — это функция тождества вида λx.x )

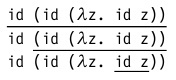
В этом терме содержится три редекса:

Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение

(λx.λy. x) z ((λx.x x)(λx.x x))

Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y . Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y , а z — первоначальный терм имел бы вид (λx.λz.x)y и после редукции выглядел бы как λz.y . Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.

Так же бывает, что у нас есть абстракция λx.t x , причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t . Такое преобразование называется η-конверсией.

На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

Лямбда-исчисление — это формальная система в математической логике для выражения подсчетов на основе абстракции и применения функций с использованием привязки и подстановки переменных. Это универсальная модель, которую можно применять для проектирования любой машины Тьюринга. Впервые введена лямбда-исчисления Черчем, известным математиком, в 1930-х годах.

Система состоит из построения лямбда-членов и выполнения над ними операций сокращения.

Пояснения и приложения

Греческая буква lambda (λ) используется в лямбда-выражениях и лямбда-терминах для обозначения связывания переменной в функции.

Лямбда-исчисление может быть нетипизировано или типизировано. В первом варианте функции могут быть применены только в том случае, если они способны принимать данные этого типа. Типизированные лямбда-исчисления слабее, могут выражать меньшее значение. Но, с другой стороны, они позволяют доказывать больше вещей.

Одной из причин того, что существует много разных типов — это желание ученых сделать больше, не отказываясь от возможности доказывать сильные теоремы лямбда-исчислений.

Система находит применение во многих различных областях математики, философии, лингвистики, и компьютерных наук. В первую очередь, лямбда-исчисления — это расчет, который сыграл важную роль в развитии теории языков программирования. Именно стили функционального создания реализуют системы. Они также являются актуальной темой исследований в теории этих категорий.

Для чайников

Лямбда-исчисление была введена математиком Алонзо Черчем в 1930-х годах в рамках исследования основ науки. Первоначальная система была показана как логически несовместимая в 1935 году, когда Стивен Клин и Дж. Б. Россер разработали парадокс Клини-Россера.

В последствии, в 1936 году Черч выделил и опубликовал только ту часть, которая имеет отношение к расчетам, то, что сейчас называется нетипизированным лямбда-исчислением. В 1940 он также представил более слабую, но логически непротиворечивую теорию, известную как система простого типа. В свое работе он объясняет всю теорию простым языком, поэтому, можно сказать, что Черч опубликовал лямбду исчисления для чайников.

До 1960-х годов, когда выяснилось его отношение к языкам программирования, λ стала лишь формализмом. Благодаря применениям Ричарда Монтегю и других лингвистов в семантике естественного языка, исчисление стало занимать почетное место как в лингвистике, так и в информатике.

Происхождение символа

Введение в лямбда исчисление

Система состоит из языка терминов, которые выбираются определенным формальным синтаксисом, и набора правил преобразования, которые позволяют манипулировать ими. Последний пункт можно рассматривать как эквациональную теорию или как операционное определение.

Все функции в лямбда-исчислении являются анонимными, то есть не имеющими имен. Они принимают только одну входную переменную, при этом каррирование используется для реализации графиков с несколькими непостоянными.

Лямбда-термины

Следующие три правила дают индуктивное определение, которое можно применять для построения всех синтаксически допустимых понятий:

Переменная x сама по себе является действительным лямбда-термином:

если T это ЛТ, и x непостоянная, то (lambda xt) называется абстракцией.
если T, а также s понятия, то (TS) называется приложением.

Ничто другое не является лямбда-термином. Таким образом, понятие действительно тогда и только тогда, когда оно может быть получено повторным применением этих трех правил. Тем не менее некоторые скобки могут быть опущены в соответствии с другими критериями.

Определение

Лямбда-выражения состоят из:

переменных v 1, v 2. v n.
символов абстракции 'λ' и точки '.'
скобок ().

Множество Λ, может быть определено индуктивно:

Если x переменная, то x ∈ Λ;
x непостоянная и M ∈ Λ, то (λx.M) ∈ Λ;
M, N ∈ Λ, то (MN) ∈ Λ.

Обозначение

Чтобы сохранить нотацию лямбда-выражений в незагроможденном виде, обычно применяются следующие соглашения:

Внешние скобки опущены: MN вместо (MN).
Предполагается, что приложения остаются ассоциативными: взамен ((MN) P) можно написать MNP.
Тело абстракции простирается дальше вправо: λx.MN означает λx. (MN), а не (λx.M) N.
Сокращается последовательность абстракций: λx.λy.λz.N можно λxyz.N.

Свободные и связанные переменные

Оператор λ соединяет свою непостоянную, где бы он ни находился в теле абстракции. Переменные, попадающие в область, называются связанными. В выражении λ x. М, часть λ х часто называют связующим. Как бы намекая, что переменные становятся группой с добавлением Х х к М. Все остальные неустойчивые называются свободными.

Множество свободных переменных M обозначается как FV (M) и определяется рекурсией по структуре терминов следующим образом:

FV (x) = , где x - переменная.
FV (λx.M) = FV (M) \ .
FV (MN) = FV (M) ∪ FV (N).

Формула, которая не содержит свободных переменных, называется закрытой. Замкнутые лямбда-выражения также известны как комбинаторы и эквивалентны терминам в комбинаторной логике.

Сокращение

Значение лямбда-выражений определяется тем, как они могут быть сокращены.

Существует три вида урезания:

α-преобразование: изменение связанных переменных (альфа).
β-редукция: применение функций к своим аргументам (бета).
η-преобразование: охватывает понятие экстенсиональности.

Здесь речь также идет о полученных эквивалентностях: два выражения являются β-эквивалентными, если они могут быть β-преобразованы в одно и то же составляющее, а α / η-эквивалентность определяется аналогично.

Термин redex, сокращение от приводимого оборота, относится к подтемам, которые могут быть сокращены одним из правил. Лямбда исчисление для чайников, примеры:

(λ x.M) N является бета-редексом в выражении замены N на x в M. Составляющее, к которому сводится редекс, называется его редуктом. Редукция (λ x.M) N есть M [x: = N].

Если x не является свободной в M, λ х. М х также ет-REDEX с регулятором М.

α-преобразование

Альфа-переименования позволяют изменять имена связанных переменных. Например, λ x. х может дать λ у. у. Термины, которые отличаются только альфа-преобразованием, называются α-эквивалентными. Часто при использовании лямбда-исчисления α-эквивалентные считаются взаимными.

Точные правила для альфа-преобразования не совсем тривиальны. Во-первых, при данной абстракции переименовываются только те переменные, которые связаны с одной и той же системой. Например, альфа-преобразование λ x.λ x. x может привести к λ y.λ x. х, но это может не ввергнуть к λy.λx.y Последний имеет иной смысл, чем оригинал. Это аналогично понятию программирования затенения переменных.

Во-вторых, альфа-преобразование невозможно, если оно приведет к захвату непостоянной другой абстракцией. Например, если заменить x на y в λ x.λ y. x, то можно получить λ y.λ y. у, что совсем не то же самое.

В языках программирования со статической областью видимости альфа-преобразование можно использовать для упрощения разрешения имен. При этом следя за тем, чтобы понятие переменной не маскировало обозначение в содержащей области.

В нотации индекса Де Брюйна любые два альфа-эквивалентных термина синтаксически идентичны.

Замена

Изменения, написанные Е [V: = R], представляют собой процесс замещения всех свободных вхождений переменной V в выражении Е с оборотом R. Подстановка в терминах λ определяется лямбдой исчисления рекурсии по структуре понятий следующим образом (примечание: x и y - только переменные, а M и N - любое λ-выражение).

y [x: = N] ≡ y, если x ≠ y

(M 1 M 2) [x: = N] ≡ (M 1 [x: = N]) (M 2 [x: = N])

(λ x.M) [x: = N] ≡ λ x.M

(λ y.M) [x: = N] y λ y. (M [x: = N]), если x ≠ y, при условии, что y ∉ FV (N).

Для подстановки в лямбда-абстракцию иногда необходимо α-преобразовать выражение. Например, неверно, чтобы (λ x. Y) [y: = x] приводило к (λ x. X), потому что замещенный x должен был быть свободным, но в итоге был связанным. Правильная замена в этом случае (λ z. X) с точностью до α-эквивалентности. Стоит обратить внимание, что замещение определяется однозначно с верностью до лямбды.

β-редукция

Бета-редукция отражает идею применения функции. Бета-восстановительный определяется в терминах замещения: ((X V. E) Е ') является Е [V: = Е'].

Например, предполагая некоторое кодирование 2, 7, ×, имеется следующее β-уменьшение: ((λ n. N × 2) 7) → 7 × 2.

Бета-редукция может рассматриваться как то же самое, что и концепция локальной сводимости при естественной дедукции через изоморфизм Карри – Ховарда.

η-преобразование

Эта-конверсия выражает идею экстенсиональности, которая в этом контексте заключается в том, что две функции равны тогда, когда они дают одинаковый результат для всех аргументов. Эта конвертация обменивает между λ x. (F x) и f всякий раз, когда x не кажется свободным в f.

Данное действие может рассматриваться как то же самое, что и концепция локальной полноты в естественной дедукции через изоморфизм Карри – Ховарда.

Нормальные формы и слияние

Для нетипизированного лямбда-исчисления β-редукция как правило переписывания не является ни сильно нормализующей, ни слабо.

Тем не менее можно показать, что β-редукция сливается при работе до α-преобразования (т. е. можно считать две нормальные формы равными, если возможно α-преобразование одной в другую).

Поэтому и сильно нормализующие члены, и слабо налаживающие понятия имеют единственную нормальную форму. Для первых терминов любая стратегия сокращения гарантированно приведет к типичной конфигурации. Тогда как для слабо нормализующих условий некоторые стратегии сокращения могут не найти ее.

Дополнительные методы программирования

Существует большое количество идиом создания для лямбда-исчисления. Многие из них были первоначально разработаны в контексте использования систем в качестве основы для семантики языка программирования, эффективно применяя их в качестве создания низкого уровня. Поскольку некоторые стили включают лямбда-исчисление (или что-то очень похожее) в качестве фрагмента, эти методы также находят применение в практическом создании, но затем могут восприниматься как неясные или чужие.

Именованные константы

В лямбда-исчислении библиотека принимает форму набора ранее определенных функций, в которой термины являются просто конкретными константами. Чистое исчисление не имеет понятия именованных неизменных, поскольку все атомные лямбда-термины являются переменными. Но их также можно имитировать, выделив непостоянную в качестве имени константы, используя лямбда-абстракцию для связывания этой изменчивой в основной части, и применить эту абстракцию к намеченному определению. Таким образом, если использовать f для обозначения M в N, можно сказать,

Авторы часто вводят синтаксическое понятие, такое как let, чтобы разрешить писать все в более интуитивном порядке.

Заметным ограничением этого let является то, что имя f не определено в M, поскольку M находится вне области привязки лямбда-абстракции f. Это означает, что атрибут рекурсивной функции не может использоваться как M с let. Более продвинутая синтаксическая конструкция letrec, которая позволяет писать рекурсивные определения функций в этом стиле, вместо этого дополнительно использует комбинаторы с фиксированной точкой.

Печатные аналоги

Данный тип является типизированным формализмом, который использует символ для обозначения анонимной функции абстракция. В этом контексте типы обычно являются объектами синтаксической природы, которые присваиваются лямбда-терминам. Точная натура зависит от рассматриваемого исчисления. С определенной точки зрения, типизированные ЛИ можно рассматривать как уточнения нетипизированного ЛИ. Но с другой стороны, их также можно считать более фундаментальной теорией, а нетипизированное лямбда-исчисление — особым случаем только с одним типом.

Типизированные ЛИ являются основополагающими языками программирования и основой функциональных, таких как ML и Haskell. И, более косвенно, императивных стилей создания. Типизированные лямбда-исчисления играют важную роль в разработке систем типов для языков программирования. Здесь типизируемость обычно захватывает желательные свойства программы, например, она не вызовет нарушения доступа к памяти.

Типизированные лямбда-исчисления тесно связаны с математической логикой и теорией доказательств через изоморфизм Карри – Говарда, и их можно рассматривать как внутренний язык классов категорий, например, который просто является стилем декартовых замкнутых.

Лямбда-выражения являются одним из наиболее мощных дополнений в C++11 и продолжают развиваться с каждым новым стандартом языка. В этой статье мы пройдемся по их истории и посмотрим на эволюцию этой важной части современного C++.

Вторая часть доступна по ссылке:
Lambdas: From C++11 to C++20, Part 2

Вступление

Я решил взять код у Томаса (с его разрешения!), описать его и создать отдельную статью.

Мы начнем с изучения C++03 и с необходимости в компактных локальных функциональных выражениях. Затем мы перейдем к C++11 и C++14. Во второй части серии мы увидим изменения в C++17 и даже взглянем на то, что произойдет в C++ 20.

С самого начала STL std::algorithms , такие как std::sort , могли принимать любой вызываемый объект и вызывать его для элементов контейнера. Однако в C++03 это предполагало только указатели на функции и функторы.

Но проблема заключалась в том, что вы должны были написать отдельную функцию или функтор в другой области видимости, а не в области видимости вызова алгоритма.

В качестве потенциального решения вы могли бы подумать о написании локального класса функторов — поскольку C++ всегда поддерживает этот синтаксис. Но это не работает…

Посмотрите на этот код:

Попробуйте скомпилировать его с -std=c++98 , и вы увидите следующую ошибку в GCC:

Если мы посмотрим на N3337 — окончательный вариант C++11, то увидим отдельный раздел для лямбд: [expr.prim.lambda].

Далее к C++11

Вот базовый пример кода, который также показывает соответствующий объект локального функтора:

Вы также можете проверить CppInsights, который показывает, как компилятор расширяет код:

Посмотрите на этот пример:

В этом примере компилятор преобразует:

Во что-то похожее на это (упрощенная форма):

Некоторые определения, прежде чем мы начнем:

Вычисление лямбда-выражения приводит к временному prvalue. Этот временный объект называется объектом-замыканием (closure object).

Тип лямбда-выражения (который также является типом объекта-замыкания) является уникальным безымянным non-union типом класса, который называется типом замыкания (closure type).

Несколько примеров лямбда-выражений:

Поскольку компилятор генерирует уникальное имя для каждой лямбды, узнать его заранее не представляется возможным.

Более того [expr.prim.lambda]:
Тип замыкания, связанный с лямбда-выражением, имеет удаленный ([dcl.fct.def.delete]) конструктор по умолчанию и удаленный оператор присваивания.

Поэтому вы не можете написать:

Это приведет к следующей ошибке в GCC:

Оператор вызова

По умолчанию это встроенный константный метод. Вы можете изменить его, указав mutable после объявления параметров:

Захватив переменную, вы создаете член-копию этой переменной в типе замыкания. Затем внутри тела лямбды вы можете получить к нему доступ.

[&] — захват по ссылке, все переменные в автоматическом хранилище объявлены в области охвата
[=] — захват по значению, значение копируется
[x, & y] — явно захватывает x по значению, а y по ссылке

Вы можете поиграться с полным примером здесь: @Wandbox

Хотя указание [=] или [&] может быть удобно — поскольку оно захватывает все переменные в автоматическом хранилище, более очевидно захватывать переменные явно. Таким образом, компилятор может предупредить вас о нежелательных эффектах (см., например, примечания о глобальных и статических переменных)

И важная цитата:

По умолчанию operator() типа замыкания является константным, и вы не можете изменять захваченные переменные внутри тела лямбда-выражения.
Если вы хотите изменить это поведение, вам нужно добавить ключевое слово mutable после списка параметров:

В приведенном выше примере мы можем изменить значения x и y… но это только копии x и y из прилагаемой области видимости.

Захват глобальных переменных

Если у вас есть глобальное значение, а затем вы используете [=] в лямбде, вы можете подумать, что глобальное значение также захвачено по значению… но это не так.

Поиграть с кодом можно здесь: @Wandbox

Захватываются только переменные в автоматическом хранилище. GCC может даже выдать следующее предупреждение:

Это предупреждение появится только в том случае, если вы явно захватите глобальную переменную, поэтому, если вы используете [=] , компилятор вам не поможет.
Компилятор Clang более полезен, так как генерирует ошибку:

Захват статических переменных

Захват статических переменных аналогичен захвату глобальных:

Поиграть с кодом можно здесь: @Wandbox

И снова, предупреждение появится, только если вы явно захватите статическую переменную, поэтому, если вы используете [=] , компилятор вам не поможет.

Захват члена класса

Знаете ли вы, что произойдет после выполнения следующего кода:

Код объявляет объект Baz, а затем вызывает foo() . Обратите внимание, что foo() возвращает лямбду (хранящуюся в std::function ), которая захватывает член класса.

Поскольку мы используем временные объекты, мы не можем быть уверены, что произойдет, при вызове f1 и f2. Это проблема висячих ссылок, которая порождает неопределенное поведение.

Опять же, если вы укажете захват явно ([s]):

Компилятор предотвратит вашу ошибку:

Move-able-only объекты

Если у вас есть объект, который может быть только перемещен (например, unique_ptr), то вы не можете поместить его в лямбду в качестве захваченной переменной. Захват по значению не работает, поэтому вы можете захватывать только по ссылке… однако это не передаст его вам во владение, и, вероятно, это не то, что вы хотели.

Сохранение констант

Если вы захватываете константную переменную, то константность сохраняется:

Возвращаемый тип

В C++11 вы можете пропустить trailing возвращаемый тип лямбды, и тогда компилятор выведет его за вас.

Первоначально вывод возвращаемого типа значения был ограничен лямбдами, содержащими один оператор return, но это ограничение было быстро снято, поскольку не было проблем с реализацией более удобной версии.

Таким образом, начиная с C++11, компилятор может вывести тип возвращаемого значения, если все операторы return могут быть преобразованы в один и тот же тип.

Если все операторы return возвращают выражение и типы возвращаемых выражений после преобразования lvalue-to-rvalue (7.1 [conv.lval]), array-to-pointer (7.2 [conv.array]) и function-to-pointer (7.3 [conv.func]) такое же, как у общего типа;

Поиграться с кодом можно здесь: @Wandbox

В вышеприведенной лямбде есть два оператора return , но все они указывают на double , поэтому компилятор может вывести тип.

IIFE — Немедленно вызываемые выражения (Immediately Invoked Function Expression)

В наших примерах я определял лямбду, а затем вызвал ее, используя объект замыкания… но ее также можно вызывать немедленно:

Такое выражение может быть полезно при сложной инициализации константных объектов.

Преобразование в указатель на функцию

Тип замыкания для лямбда-выражения без захвата имеет открытую невиртуальную неявную функцию преобразования константы в указатель на функцию, имеющую тот же параметр и возвращаемые типы, что и оператор вызова функции типа замыкания. Значение, возвращаемое этой функцией преобразования, должно быть адресом функции, которая при вызове имеет тот же эффект, что и вызов оператора функции типа сходного с типом замыкания.

Другими словами, вы можете преобразовывать лямбды без захватов в указатель на функцию.

Поиграться с кодом можно здесь: @Wandbox

Улучшения в C++14

C++14 добавил два значительных улучшения в лямбда-выражения:

Захваты с инициализатором
Общие лямбды

Возвращаемый тип

Вывод типа возвращаемого значения лямбда-выражения был обновлен, чтобы соответствовать правилам автоматического вывода для функций.

Возвращаемый тип лямбды — auto, который заменяется trailing возвращаемым типом, если он предоставляется и/или выводится из операторов возврата, как описано в [dcl.spec.auto].

Захваты с инициализатором

Короче говоря, мы можем создать новую переменную-член типа замыкания и затем использовать ее внутри лямбда-выражения.

Это может решить несколько проблем, например, с типами, доступными только для перемещения.

Перемещение

Теперь мы можем переместить объект в член типа замыкания:

Оптимизация

Другая идея состоит в том, чтобы использовать его как потенциальную технику оптимизации. Вместо того, чтобы вычислять какое-то значение каждый раз, когда мы вызываем лямбду, мы можем вычислить его один раз в инициализаторе:

Захват переменной-члена

Инициализатор также можно использовать для захвата переменной-члена. Затем мы можем получить копию переменной-члена и не беспокоиться о висячих ссылках.

Поиграться с кодом можно здесь: @Wandbox

В foo() мы захватываем переменную-член, копируя ее в тип замыкания. Кроме того, мы используем auto для вывода всего метода (ранее, в C++11 мы могли использовать std::function ).

Обобщенные лямбда-выражения

Еще одно существенное улучшение — это обобщенная лямбда.
Начиная с C++14 можно написать:

Это эквивалентно использованию объявления шаблона в операторе вызова типа замыкания:

Такая обобщенная лямбда может быть очень полезна, когда трудно вывести тип.

В этой статье мы начали с первых дней лямбда-выражений в C++03 и C++11 и перешли к улучшенной версии в C++14.

Вы увидели, как создавать лямбду, какова основная структура этого выражения, что такое список захвата и многое другое.

В следующей части статьи мы перейдем к C++17 и познакомимся с будущими фичами C++20.

Вторая часть доступна здесь:

А сегодня немного теории. Я не считаю, что лямбда-исчисление является необходимым знанием для любого программиста. Однако, если вам нравится докапываться до истоков, чтобы понять на чем основаны многие языки программирования, вы любознательны и стремитесь познать все в этом мире или просто хотите сдать экзамен по функциональном программированию (как, например, я), то этот пост для вас.

Что это такое

Лямбда-исчисление - это формальная система, то есть набор объектов, формул, аксиом и правил вывода. Благодаря таким системам с помощью абстракций моделируется теория, которую можно использовать в реальном мире, и при этом выводить в ней новые математически доказуемые утверждения. Например, язык запросов SQL основан на реляционном исчислении. Благодаря математической базе, на которой он существует, оптимизаторы запросов могут анализировать алгебраические свойства операций и влиять на скорость работы.

Но речь сегодня не о SQL, а о функциональных языках. Именно для них лямбда-исчисление является основой. Функциональные языки далеко не столь популярны, как, например, объектно-ориентированные, но тем не менее прочно занимают свою нишу. Кроме того, многие идеи из функционального программирования и лямда-исчисления постепенно прокрадываются в другие языки, под видом новых фич.

Если вы изучали формальные языки, то знаете о таком понятии как Машина Тьюринга. Эта вычислительная абстракция определяет класс вычислимых функций. Этот класс столь важен, так как по тезису Черча он эквивалентен понятию алгоритма. Другими словами, любую программу, которую можно запрограммировать на вычислительном устройстве, можно воспроизвести и на машине Тьюринга. А для нас главное то, что лямбда-исчисление по мощности эквивалентно машине Тьюринга и определяет этот же класс функций. Причем создателем лямбда-исчисления является тот самый Алонзо Черч!

Основные понятия

В нотации лямбда-исчисления есть всего три типа выражений:

Переменные: ` x, y, z `
Абстракция - декларация функции: ` lambda x.E ` . Определяем функцию с параметром ` x ` и телом ` E `.
Аппликация - применение функции ` E_1 ` к аргументу ` E_2 ` : ` E_1 E_2`

Сразу пара примеров:

Тождественная функция: ` lambda x. x `
Функция, вычисляющая тождественную функцию: ` lambda x.(lambda y . y) `

Соглашения

Несколько соглашений для понимания, в каком порядке правильно читать выражения:

Аппликация лево-ассоциативна. То есть выражение ` x y z ` читается как ` (x y) z `.
В абстракции группируем скобки вправо. Другими словами, читая абстракцию необходимо распространять ее максимально вправо насколько возможно. Пример: выражение ` lambda x. x \ lambda y . x y z ` эквивалентно ` lambda x. (x \ (lambda y . ((x y) z))) ` , так как абстракция функции с аргументом ` x ` включила в себя все выражение. Следом было проведено включение абстракцией с аргументом ` y ` и ,наконец, в теле этой функции были расставлены скобки для аппликации.

Области видимости переменных

Определим контекст переменной, в котором она может быть использована. Абстракция ` lambda x.E ` связывает переменную ` x `. В результате мы получаем следующие понятия:

` x ` - связанная переменная в выражении .
` E ` - область видимости переменной ` x `.
Переменная свободна в ` E ` , если она не связана в ` E ` . Пример: ` lambda x. x (lambda y. x y z) ` . Cвободная переменная - ` z ` .

Взглянем на следующий пример: ` lambda x. x (lambda x. x) x ` .

Понимание лямбда-выражений существенно усложняется, когда переменные с разными значениями и контекстами используют идентичные имена. Поэтому впредь мы будем пользоваться следующим соглашением: связанные переменные необходимо переименовывать для того, чтобы они имели уникальные имена в выражении. Это возможно благодаря концептуально важному утверждению: выражения, которые могут быть получены друг из друга путем переименования связанных переменных, считаются идентичными. Важность этого утверждения в том, что функции в исчислении определяются лишь своим поведением, и имена функций не несут никакого смысла. То есть, функции ` lambda x. x ` , ` lambda y. y ` , ` lambda z. z ` на самом деле одна тождественная функция.

Вычисление лямбда-выражений

Вычисление выражений заключается в последовательном применении подстановок. Подстановкой ` E’ ` вместо ` x ` в ` E \ ` (запись: ` [E’//x]E ` ) называется выполнение двух шагов:

Альфа-преобразование. Переименование связанных переменных в ` E ` и ` E’ ` , чтобы имена стали уникальными.
Бета-редукция. По сути единственная значимая аксиома исчисления. Подразумевает замену ` x ` на ` E’ ` в ` E ` . Рассмотрим несколько примеров подстановок:

Преобразование к тождественной функции. ` (lambda f. f (lambda x. x)) (lambda x. x) -> ` (пишем подстановку) ` -> [lambda x. x // f] f ( lambda x. x)) = ` (делаем альфа-преобазование) ` = [(lambda x. x) // f] f (lambda y. y)) = ` (производим бета-редукцию) ` = (lambda x. x) (lambda y. y) -> ` (еще одна подстановка) ` -> [lambda y. y // x] x = lambda y. y `
Бесконечные вычисления. ` (lambda x. x x)(lambda x. x x) -> [lambda x. x x // x]x x = [lambda y. y y // x] x x = ` ` = (lambda y. y y)(lambda y. y y) -> … `
Также небольшой пример, почему нельзя пренебрегать альфа-преобразованием. Рассмотрим выражение ` (lambda x. lambda y. x) y ` . Если не выполнить первый шаг, результатом будет тождественная функция ` lambda y. y ` . Однако, после правильного выполнения подстановки с заменой ` y ` на ` z ` мы получим совсем другой результат ` lambda z. y ` , то есть константную функцию.

Функции нескольких переменных

Для того чтобы использовать функции нескольких переменных добавим в исчисление новую операцию ` add ` : она применяется к двум аргументам и является синтаксическим сахаром для следующих вычислений: ` (lambda x. lambda y. add \ x y) E_1 E_2 -> ([E_1 // x] lambda y. add \ x y) E_2 = ` ` (lambda y. add \ E_1 y) E_2 -> ` ` [E_2 // y] add \ E_1 y = add \ E_1 E_2 `

Как результат мы получили функцию от одного аргумента, которая возвращает еще одну функцию от одного аргумента. Такое преобразование называется каррирование (в честь Хаскелла Карри назвали и язык программирования, и эту операцию), а функция, возвращающая другую, называется функцией высшего порядка.

Порядок вычислений

Бывают ситуации, когда произвести вычисление можно несколькими способами. Например, в выражении ` (lambda y. (lambda x. x) y) E ` сначала можно подставлять ` y ` вместо ` x ` во внутреннее выражение, либо ` E ` вместо ` y ` во внешнее. Теорема Черча-Рассера говорит о том, что в не зависимости от последовательности операций, если вычисление завершится, результат будет одинаков. Тем не менее, эти два подхода принципиально отличаются. Рассмотрим их подробнее:

Вызов по имени. В вычислении всегда в первую очередь применяются самые внешние подстановки. Другими словами, нужно вычислять аргумент уже после подстановки в функцию. Кроме того нельзя использовать редукцию внутри абстракции. Пример: ` (lambda y. (lambda x. x) y) ((lambda u. u) (lambda v. v)) -> ` (применяем редукцию к внешней функции) ` -> (lambda x. x) ((lambda u. u) (lambda v. v)) -> ` (вновь подставляем, не меняя аргумент) ` -> (lambda u. u) (lambda v. v) = lambda v. v `
Вызов по значению. В этом способе вычисление проходит ровно наоборот, то есть сначала вычисляется аргумент функции. При этом редукция внутри абстракции также не применяется. Пример: ` (lambda y. (lambda x. x) y) ((lambda u. u) (lambda v. v)) -> ` (вычисляем аргумент функции) ` -> (lambda y. (lambda x. x) y) (lambda v. v) -> (lambda x. x) (lambda v. v) -> lambda v. v `

Из практических отличий этих двух подходов отметим, то что вычисление по значению более сложно в реализации и редко используется для всех вычислений в неисследовательских языках. Однако, второй подход может не привести к завершению вычисления. Пример: ` (lambda x. lambda z.z) ((lambda y. y y) (lambda u. u u)) ` . При вычислении аргумента мы попадаем в бесконечный цикл, в то время как, проводя вычисления по имени функции, мы сразу получим тождественную функцию.

Кодирование типов

В чистом лямбда-исчислении есть только функции. Однако, программирование трудно представить без различных типов данных. Идея заключается в том, чтобы закодировать поведение конкретных типов в виде функций.

Булевые значения. Поведение типа можно описать как функцию, выбирающую одно из двух. Тогда значения выглядят так: ` true = lambda x. lambda y. x ` и ` false = lambda x. lambda y. y `
Натуральные числа. Каждое натуральное число может быть описано как функция, проитерированная заданное число раз. Выпишем несколько первых чисел ( ` f ` - функция, которую итерируем, а ` s ` - начальное значение):
- ` 0 = lambda f. lambda s. s `
- ` 1 = lambda f. lambda s. f s `
- ` 2 = lambda f. lambda s. f (f s) `
Операции с натуральными числами.
- Следующее число. ` \s\u\c\c \ n = lambda f. lambda s. f (n f s) ` . Аргумент функции - число ` n ` , которое, будучи так же функцией, принимает еще два аргумента: начальное значение и итерируемую функцию. Для числа ` n ` один раз применяем функцию ` f ` и получаем следующее число.
- Сложение. ` add \ n_1 n_2 = n_1 \ \s\u\c\c \ n_2 ` . Для сложения чисел ` n_1 ` и ` n_2 ` нужно одному из слагаемых передать в параметры функцию ` \s\u\c\c `, как итерруемую функцию, и другое слагаемое, как начальное значение. В результате мы увеличим заданное число на единицу необходимое число раз.
- Умножение. ` \m\u\l\t \ n_1 n_2 = n_1 (add \ n_2) 0 ` . В роли итерируемой функции для множителя ` n_1 ` выступает функция ` \s\u\c\c ` с аргументом ` n_2 ` , а в роли начального значения уже определенное число ` 0 ` . То есть мы определяем умножение как прибавление ` n_2 ` к нулю ` n_1` раз.

Аналогично, с помощью лямбда-исчисления можно выразить любые конструкции языков программирования, такие как циклы, ветвления, списки и тд.

Заключение

Лямбда-исчисление - очень мощная система, которая позволяет писать любые программы. Однако, непосредственно программирование на лямбда-исчислении получается черезчур громоздким и неудобным. Тем не менее, чистое лямбда-исчисление предназначено вовсе не для программирования на нем, а для изучения существующих и создания новых языков программирования. А следующим шагом на пути к типовым функциональным языкам является типизированное лямбда-исчисление - расширение чистого исчисления типовыми метками.

Читайте также: