K 2pi лямбда что это

Добавил пользователь Евгений Кузнецов
Обновлено: 07.08.2024

Волновое уравнение — линейное гиперболическое уравнение в частных производных, описывающее колебательные процессы в сплошных средах и электромагнетизме:

Где $\triangle$ — оператор Лапласа, u=u(x,t) — дифференцируемая функция, $x\in\mathbb^n$ — аргумент функции u в виде n-мерной переменной, t — время, v — фазовая скорость.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Волновые уравнения в математической физике применяются для описания малых поперечных колебаний струны и мембраны, акустических процессов в газообразных, жидких и твёрдых средах, электромагнитных и гравитационных волн.

Общий вид

Составляющие уравнения

При работе с физическими процессами в трёхмерном пространстве волновое уравнение получается из уравнения плоской волны.

Если мы имеем уравнение плоской волны:

$A(\overrightarrow r,\;t)\;=\;A_0\cos(wt\;-\;(\overrightarrow k,\overrightarrow r)\;+\;\varphi_0)$

Где $A(x,\;t)\;$ — возмущение в точке x в момент времени t, $A_0$ — волновая амплитуда, $\omega$ — круговая частота, $\overrightarrow k$ — волновой вектор, $\overrightarrow k\;=\;\overrightarrow k(x,y,z)$ — радиус-вектор в точке $x, y, z, \varphi_0$ — начальная фаза колебаний.

Если мы продифференцируем его по переменным x, y, z и t, то получим систему уравнений в частных производных:

При сложении уравнений (2), (3), (4) получаем:

Из уравнений (1) и (5) следует, что:

Таким образом, мы получаем общее волновое уравнение из суммы уравнений плоской волны в частных производных.

Для уравнений в n-мерных пространствах для построения берется система дифференциальных уравнений в частных производных по времени t и по каждому из n измерений.

Для одномерного пространства данное уравнение называется уравнением колебания струны и имеет следующую характеристику:

Из описанного выше мы можем сделать вывод, что в общем случае для решения волновых задач необходимо применение численных методов. Тем не менее, для некоторых случаев существуют аналитические решения уравнений.

Операторы уравнения

С применением оператора Лапласа уравнение (7) принимает привычный нам вид:

Оператором Д'Аламбера $\square$ называется следующая разность:

Тогда волновое уравнение можно представить в виде:

Решение уравнения

В математической физике существуют несколько частных случаев волновых уравнений, для которых существуют аналитические решения:

формула Д'Аламбера;
формула Пуассона-Парсенваля;
формула Кирхгофа.

Формула Д'Аламбера

Рассмотрим формулу Д'Аламбера, являющейся частным случаем волновых уравнений в одномерном пространстве:

Где f=f(x,t) — вынуждающая внешняя сила, $u(x,0)\;=\;\varphi(x),\;u_t(x,0)=\psi(x)$ — начальные условия.

Тогда решение формулы Д'Аламбера имеет вид:

Формула Пуассона-Парсенваля

Частным случаем волнового уравнения для поверхности или плоскости является формула Пуассона-Парсенваля.

Где $u(x,0)=\varphi(x),\;u_t(x,0)=\psi(x)$ — начальные условия.

Тогда решение формулы Пуассона-Парсенваля имеет следующий вид:

Формула Кирхгофа

В трёхмерном пространстве частным случаем волновых уравнений, для которых существует аналитическое решение, является формула Кирхгофа.

Мы имеем уравнение следующего вида:

Где $u=u(x,t), f=f(x,t), u,\;f\;\in\mathbb^n\times\mathbb^+, \bigtriangleup$ — оператор Лапласа, при начальных условиях:

Мы получим следующее решение уравнения:

Где $S:\;\vert x-y\vert=at $ — сфера, по которой осуществляется интегрирование.

Решение в сферических координатах

Стандартное волновое уравнение в сферических координатах имеет следующий вид:

Требуется найти решение данного в обычной форме:

Используя в изначальном уравнении данную формулу, а также воспользовавшись методом разделения переменных, получаем:

Посредством преобразований получаем следующую систему уравнений:

Тогда, для любых $\lambda_n=n(n+1),\;n\in\mathbb+$ имеет место:

Для удобства дальнейших вычислений произведём замену функции f(r) на R(r):

Где $R_n(r)=Z_(kr), а Z_(r)$ — решение уравнения Басселя с параметром $p=n+\frac12.$

Тогда мы получаем следующее выражение:

Волновое уравнение механических волн

Механические волны — упругие возмущения, распространяемые в упругой среде.

Рассматривают поперечные и продольные механические волны.

В продольных волнах колебания, несущие эту волну, осуществляется по вектору, параллельном направлению движения. Они возможны в газообразной, жидкой и твёрдой среде. Особенностью поперечных волн является возможность их наличия исключительно при возможности деформации сдвига в твёрдых средах.

В условиях распространения в бесконечной натянутой струне поперечная монохроматическая волна может быть описана следующим выражением (уравнением бегущей струны):

$\xi(t,z)=A\cdot\cos\omega(t-\frac zv) (23)$

Где $\xi(t,z)$ — смещение частицы из положения равновесия в струне, z — расстояние от начала струны до точки равновесного положения частицы в струне, v — скорость распространения колебаний.

Примеры задач и решение

Найти скорость распространения звуковой волны, если частота колебаний равна $\nu$ =400Гц, а амплитуда $A=10^м$ и длина волны $\lambda$ =0,8м. Также определить максимальную скорость частиц в данной среде.

Ввиду недостаточно строгого определения условий, сделаем допущение, что волна является плоской.

Тогда, сориентировав ее распространение по оси X, получим следующее уравнение:

Зная, что длина волны равна $\lambda=\frac v\nu,$ получаем, что скорость волны равна:

Исходя из того, что скорость есть первая производная расстояния по времени, имеем:

$\frac=\frac d(A\cos\omega(t-\frac x\nu))=-A\omega\sin\omega(t-\frac x\nu),$ следовательно:

Скорость распространения волны по упругой струне составляет $\nu$ =10 м/с. Амплитуда колебаний точек в струне составляет A=0,05 м, период колебаний составляет Т=1 с. Сформулировать уравнение волны.

Так как в общем случае при распространении по оси X уравнение поперечной механической волны имеет вид:

то, найдя циклическую частоту по формуле $\omega=\frac<2\pi>T=2\pi\;(рад/с),$ получаем:

Рассматривая законы распространения механических волн, отвлекаются от молекулярного строения вещества, рассматривая его как сплошную среду, которая непрерывно изменяется в пространстве. Говоря о частице среды, мы будем говорить о малом элементе объема вещества, размеры которого много больше, чем расстояния между молекулами, при этом частицы среды будем считать точками.

В первом приближении все вещества можно считать упругими (исключение - разреженные газы), поскольку внутренние силы, появляющиеся при малых деформациях, пропорциональны величинам деформации.

Если в какой - то точке упругой среды возбудить колебания ее частиц, из-за их взаимодействия оно будет распространяться в веществе от одной частицы к другой с некоторой скоростью. Процесс распространения колебаний в пространстве называют волной. При этом частицы среды волной не переносятся, а каждая частица совершает колебания около своего положения равновесия.

В зависимости от направления колебаний частицы вещества по отношению к направлению распространения волны, волны делят на продольные и поперечные. Если частицы совершают колебания в направлении распространения волны, то такую волну называют продольной.

Определение поперечных волн

Поперечной волной называют такую волну, в которой колебания частиц среды происходят в направлениях перпендикулярных к направлению распространения волны.

Механические волны могут быть поперечными только в среде, в которой возможны деформации сдвига (среда обладает упругостью формы). Следовательно, в жидкостях и газах механических поперечных волн не наблюдают. Поперечные механические волны возникают в твердых телах. Примером таких волн являются волны, которые распространяются в струнах.

Поперечная волна имеет поляризацию (линейную, круговую или эллиптическую), вектор амплитуды этой волны обладает определенной ориентацией в поперечной плоскости.

Скорость распространения поперечных волн

Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде можно найти при помощи формулы:

где $G$ - модуль сдвига среды; $\rho $ - плотность вещества.

Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.

Скорость в формуле (1) называется фазовой скоростью.

Уравнение волны

Основная задача при изучении волн - это установления закона изменения во времени и пространстве физических величин, которые однозначно характеризуют движение волны. При рассмотрении упругих волн такой величиной служит, например, смещение ($s$) частиц среды от их положений равновесия. Функция $s$ в зависимости от координат пространства и времени называется уравнением волны.

Самым простым видом волн являются гармонические волны. В таких волнах параметры $s$ для всех частиц среды, которые охвачены волной, совершают гармонические колебания с одинаковыми частотами. Для реализации данного волнового процесса необходимо, чтобы источник гармонических волн совершал незатухающие гармонические колебания.

Пусть одномерная поперечная волна распространяется по оси X , от источника волны, находящегося в начале координат - точке О. Примером такой волны является, волна, которая распространяется в упругой бесконечной струне, один из концов которой заставляют совершать колебательные движения. Если колебания в точке О происходят по закону:

где $A_0$ - амплитуда; $\omega $- циклическая частота колебаний; $\varphi $ - начальная фаза. Тогда колебания в некоторой произвольной точке А на оси X отстают по фазе от $s_0$ и происходят по закону:

где $t_1=\frac$ - время, которое необходимо для того, чтобы волна прошла расстояние от источника волны до рассматриваемой точки А ($ОА=x$). $A$ - амплитуда волны в точке А. Если среда в которой распространяется волна не поглощает энергию, то амплитуды колебаний и амплитуда волны совпадают:

Уравнение одномерной волны (3) часто записывают в другой форме, вводя понятие волнового числа ($k$):

где $\lambda $ - длина волны.

Уравнения (3) и (5) эквивалентны и называются уравнением одномерной волны.

Величина $\left[\omega t-kx+\varphi \right]$ называется фазой волны в произвольной точке А. Из сравнения уравнения (2)и уравнения (5), следует, что колебания в точке А отстают от колебаний в источнике (точке О) по фазе на величину $kx$. Величина $\left(kx+\varphi \right)$ - начальная фаза колебаний в точке А.

Расстояние между двумя ближайшими точками среды, в которых разность начальных фаз колебаний равна $2\pi $, называют длиной волны ($\lambda $).

Примеры задач с решением

Задание: Поперечная одномерная волна имеет период T и амплитуду колебаний A. Распространяется она со скоростью $v$. Каково смещение частицы среды, которая находится на расстоянии $x_1$ от источника волн в момент времени $t_1$ от начала колебаний? Изобразите рассматриваемую волну распространяющейся вдоль оси X для фиксированного момента времени ($t_1$).

Решение: Запишем уравнение одномерной волны, которое даст нас смещение частицы среды:

Будем считать что в начальный момент времени начальная фаза колебаний равна нулю ($\varphi $=0). Циклическую частоту найдем, зная период колебаний точек в волне:

Волновое число равно:

Перепишем уравнение волны (1.1) учитывая (1.2) и (1.3):

Для того чтобы найти смещение заданной в условии задачи точки, которую определяет параметр ($x_1$) в момент времени $t_1$, подставим эти параметры в уравнение (1.4) получаем:

Задание: Покажите, что уравнение одномерной волны удовлетворяет волновому уравнению:

Решение: Запишем уравнение одномерной волны:

Найдем произведение $\frac\frac<<\partial >^2s><\partial t^2>,$ используя (2.4) и условие задачи $\omega =kv$:

Сравниваем правые части уравнений (2.3) и (2.5):

Получаем, если правые части равны, то равны и левые:

Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Длиной волны называют кратчайшее пространственное расстояние между ее точками, совершающими колебания в одной фазе. Обозначают длину волны, чаще всего буквой $\lambda$ .

Для синусоидальных волн $\lambda$ – это расстояние, на которое волна распространяется за один период (T). Длину волны в этом случае еще называют пространственным периодом. Тогда формулой длины волны можно считать выражение:

где v – скорость распространения волны, $\nu=\frac$ – частота колебаний, $k=\frac<\omega>$ – волновое число, $T=\frac<\omega>$ – период волны, $\omega$ – циклическая частота волны.

Длина стоячей волны

Длиной стоячей волны($\lambda_$) называют расстояние в пространстве между двумя пучностями (или узлами):

где $\lambda$ – длина бегущей волны. Надо заметить, что расстояние между соседними пучностью и узлом связывает равенство:

Длина бегущей волны

В бегущей волне длина волны связана с фазовой скоростью (v_ph) формулой:

Длина бегущей волны

Разность фаз и длина волны

Две точки волны находящиеся на расстоянии $\Delta x$ имеют при колебании разность фаз ($\Delta \varphi$), которая равна:

Длина электромагнитной волны

Скорость распространения электромагнитных волн в вакууме равна скорости света в вакууме ($c \approx 3 \cdot 10^$ м/с), следовательно, длина электромагнитной волны в вакууме, может быть рассчитана при помощи формулы:

Длина электромагнитной волны в веществе равна:

где $n=\sqrt$ – показатель преломления вещества, $\varepsilon$ – диэлектрическая проницаемость вещества, $\mu$ – магнитная проницаемость вещества.

Отметим, что все рассматриваемые формулы относят к случаю T=const.

Единицы измерения длины волны

Основной единицей измерения длины волны в системе СИ является: [$\lambda$]=м

Примеры решения задач

Задание. Каково приращение длины электромагнитной волны, имеющей частоту v=1 МГц при ее переходе в немагнитную среду, которая имеет диэлектрическую проницаемость $\varepsilon$=2?

Решение. Так как речь в условии задачи идет о немагнитной среде, в которую переходит волна, то считаем магнитную проницаемость вещества равной единице ($\mu$=1).

Длина рассматриваемой нами волны в вакууме равна:

Длина волны в веществе:

Используя выражения (1.1) и (1.2) найдем изменение длины волны:

Проведем вычисления, если нам известно помимо данных приведенных в условии задачи, что $c \approx 3 \cdot 10^$ м/с- скорость света в вакууме, и v=1 МГц=10 6 Гц:

Ответ. Длина волны уменьшится на 150 м

Задание. Какова длина плоской синусоидальной волны, которая распространяется по оси X. Две точки, которые находятся на оси X расположенные на расстояниях 2 м и 3 м от источника совершают колебания с разностью фаз равной $\Delta \varphi=\frac$ . Каким будет период колебаний в волне, если ее скорость в данной среде равна v=2м/с?

Решение. Сделаем рисунок.

Основой для решения задачи будет формула:

Выразим из (2.1) искомую длину волны, получим:

Период колебаний связан с длиной волны формулой:

C учетом (2.2), имеем:

Ответ. $\lambda \approx 3,3 \mathrm ; T \approx 1,67 \mathrm$

Дифракционная решетка - оптическое устройство, представляющее собой совокупность большого числа параллельных щелей, равноудаленных друг от друга.

Суммарная ширина щели и штриха (a+b=d) – период решетки.

! d=((a+b)*N)/N=C/N!, где С –ширина решетки, N -число штрихов на ней.

на нем: Л- линза; Р – решетка; Э - экран

Максимумы, которые образуются на экране, после интерференции вторичных волн, идущих от узких щелей, удовлетворяют условию:

!d*sin фи = k*лямбда! - формула дифракционной решетки.

фи - угол дифракции (угол отклонения от прямолинейного направления);

k - порядок спектра;

лямбда - длина волны света, освещающего решетку,

Дифракционные спектры для монохроматического света представляет собой чередование максимумов и минимумов по обе стороны от центрального механизма. Максимумы имеют цвет соответствующей длины света, освещающего решетку.

Если решетку освещать белым светом, то центральный максимум будет белым, а остальные будут представлять собой чередование цветных полос плавно переходящих друг в друга, т. к. sin фи= k*лямбда/d - зависит от длины волны света. D = к/t - угловая дисперсия решетки. R =k*N - разрешающая способность.

Диффузия в жидкости. Уравнение Фика. Уравнение диффузии для мембран.

Диффузия - самопроизвольное проникновение молекул одного вещества между молекулами других.

Явление диффузии - важный элемент диффракционирования мембран. При диффузии происходит перенос массы вещества. В биофизике это называется транспорт частиц. Основным уравнением диффузии является уравнение Фика:

где I – плотность частиц при диффузии в жидкость.

D – коэффициент диффузии.

Коэффициент 1/3 возник ввиду трехмерного пространства и хаоса в движении молекул (в среднем в каждом из 3-х направлений перемещается 1/3 часть всех молекул)

сигма - средняя длина свободного пробега молекул

тау -среднее время оседлой жизни молекул

С- массовая концентрация молекул

Х- перемещение молекул вдоль оси X

- градиент массовой концентрации

Уравнение диффузии можно записать в виде:

n – концентрация молекул.

Градиент концентрации

R- универсальная газовая постоянная; Т- абсолютная температура градиент химического потенциала,

Тогда

С - концентрация частиц. А Эйнштейн показал, что D пропорционально Т. Дня биологических мембран уравнение Фика имеет вид:

- концентрация молекул внутри клеток

- коэффициент проницаемости

l – толщина мембраны.

Дифракция света на щелях.

Дифракцией света называют явление отклонения света от прямолинейного распространения в среде с резкими неоднородностями.
Описать картину дифракции можно с учетом интерференции вторичных волн.

Рассмотрим дифракцию от узкой щели (АВ)

MN – непрозрачная преграда;

АВ=а – ширина щели;

АВ – часть волновой поверхности, каждая точка которой является источником вторичных волн, которые распространяются за щелью по разным направлениям. Линза соберет лучи А, А₁ и В в точке О₁ экрана.

АD - перпендикуляр к направлению пучка вторичных волн. Разбили ВD на отрезки =лямда/2.

АА₁, А₁В - зоны Френеля. Вторичные волны, идущие от двух соседних зон Френеля, не гасят друг друга, так как отличаются по фазе на пи. Число зон, укладывающихся в щели, зависит от длины волны лямда и угла альфа.

Если щель АВ разбить при построении на нечетное число зон Френеля, а ВD на нечетное число отрезков, равных лямда/2, то в точке О₁ наблюдается максимум интенсивности света. ВD=а*sinα=+-(2k+1)*лямда/2.

Если щель разбить на четное число зон Френеля, то наблюдается минимум освещенности: а*sinα=+-2k*лямда/2=+-k*лямда.

Поэтому на экране получится система светлых (mах) и темных (min) полос симметричных относительно центра (альфа=треугольник - изменение) - наиболее яркой полосы.

Интенсивность остальных максимумов убывает с увеличением к.

3аконы излучения абсолютно чёрного тела (Стефана - Больцмана, Вина). Формула Планка. Использование термографии в диагностике.

Излучение чёрного тела имеет сплошной спектр. Графически это выглядит для разных температур так:

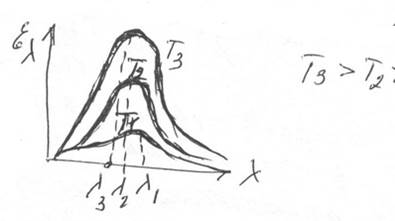
Существует максимум спектральной светимости, который при повышении

температуры смещается в сторону коротких волн.

По мере нагревания чёрного тела его энергетическая светимость (Re)

увеличивается: Re = опред интеграл от 0 до бескон от Eлямда*dлямда

Стефан и Больцман установили, что Re=сигма*T^4

Сигма = 5,6696*10^-8 Вт/K*м^2 - постоянная Стефана-Больцмана,

T=t+273 - абсолютная (термодинамическая) температура по шкале

Кельвина. Все замечали это на практике, чем выше температура спирали, нагретой печи, тем больше они излучают тепла.

Планк получил формулу для спектральной плотности абсолютно черного тела (Eлямда) и серого тела (r лямда) (лямда-индекс): Eлямда=2п*h*c^2/лямда^5 * 1/exp[h*c/k*T*лямда-1]

альфа - коэффициент поглощения

h - постоянная Планка;

С - скорость света в вакууме;

лямда - длина волны;

k - постоянная Больцмана;

Т - абсолютная температура.

2 Затухающие колебания и декремент затухания. Апериодические колебания.

Свободные колебания (происходящие без внешнего воздействия периодически действующей силы) являются затухающими. График затухающих колебаний имеет вид:

Амплитуда колебаний с каждым разом убывает. Затуханию способствуют силы трения и сопротивления, возникающие в средах. Пусть r-коэффициент трения, характеризующий свойство среды оказывать сопротивление движению. Тогда БЕТТА= r/2m – коэффицент затухания.

Wo= корень(K/m) – циклическая частота собственных колебаний, тогда W^2=Wo^2-БЕТТА^2, где W – циклическая частота затухания колебаний.

Быстрота затухания колебаний определяется коэффициентом затухания. Уравнение затухающих колебаний имеет вид А=Ао*l в степени минус бета*t

Ao – первоначальная амплитуда, А-амплитуда затухающих через время t.

Лямда=lnA(t)/A(t+T)=lnAo*(e в степени минус бета*t)/Ao*e^-бета*(t+T)=ln(e^ бета*t) –логарифмический декрет затухания.

!Лямда=бета*Т!- связь логарифмического декремента затухания с коэффициентом затухания. При сильно затухании колебания становятся апериодическими (если бета^2>Wo^2)

№31 Импеданс полной цепи переменного тока. Сдвиг фаз. Резонанс напряжения.

Рассмотрим последовательно соединенные R, L, C.

При последовательном соединении:

1) Uвх=U0*cosW*t=Ur+Ul+Uc – входное напряжение.

2) I=I0*cos(W*t-фи) – сила тока в цепи.

Начертим векторную диаграмму:

Ur0 – совпадает по фазе с силой тока;

Ul0 – опережает на пи/2;

Uc0 – отстает от тока на пи/2.

По теореме Пифагора: (U0)^2=(U0r)^2+(U0l-U0c)^2

Сократив обе части уравнения на (I0)^2 получим выражение для полного сопротивления (Z):

Z=квадратный корень из (R^2+(W*L-1/W*c)^2) – импеданс.

Если сопротивление катушки Xl= W*L равно сопротивлению конденсатора Xc=1/W*c, то полное сопротивление Z=R; по закону Ома Iрез=U0/Z=U0/R (Iрез – резонансный ток) – сила тока резко возрастает – РЕЗОНАНС. При этом Ul=Uc>>U0 – резонанс напряжений. Это возможно, т.к. Ul и Uc сдвинуты по фазе между собой на пи:

При этом на резисторе R выделяется максимальное количество теплоты:

№32 Импенданс тканей организма. Эквивалентная Электрическая схема. Оценка жизнеспособности тканей и органов но частотной зависимости к углу сдвига фаз.

Ткани организма проводят как постоянный так и переменный ток. Биологическая мембрана а значит и весь организм обладает емкостным сопротивлением, т.к. обладают емкостью, т.е. способны

накапливать заряд. При пропускании через живые ткани переменного тока наблюдается отставание напряжения от тока. Омические емкостные свойства биологических тканей можно моделировать используя эквивалентные электрические схемы, при любых частотах зависимость сдвига фаз и импенданса от частоты выполняется для схемы

1/Zв2=1/Rв2+1/корень(R1 в2+1/Wв2*Св2)!, где Z-полное сопротивление данной цепи, с - ёмкость.

При малых частотах: Z=R2 При больших частотах: Zmin=(R1*R2)/(R1+R2).

Графическое изображение зависимости импенданса живой ткани от частоты переменного тока.

Сдвиг фаз между током и напряжением tg фи = R/Xc=RWC (1).

Частотная зависимость сдвига фаз живой ткани. При отмирании ткани натрий-калиевый канал биологических мембран разрушается, цитоплазма

клетки (проводник) соединяется с межклеточной

жидкостью(проводник) и емкостные свойства ткани уменьшаются, а это значит, что и импенданс (Z) и сдвиг фаз (фи) меньше зависят от частоты. Мёртвая ткань обладает лишь омическим сопротивлением (R), и не зависит от частоты. Диагностический метод, основанный на регистрации изменения импенданса тканей и сдвига фаз называется РЕОГРАФИЕЙ.

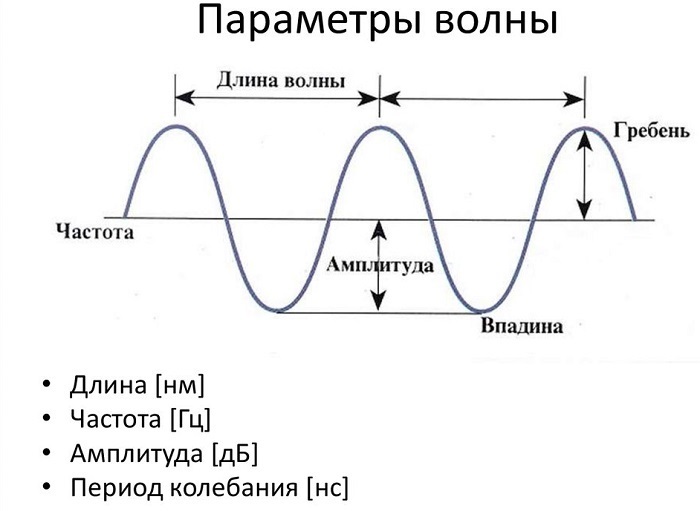
Длина волны - это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.

Цикл - это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.

На рисунке показаны основные параметры волны, используемые в физике:

Определение и формула длины волн

Волна - это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.

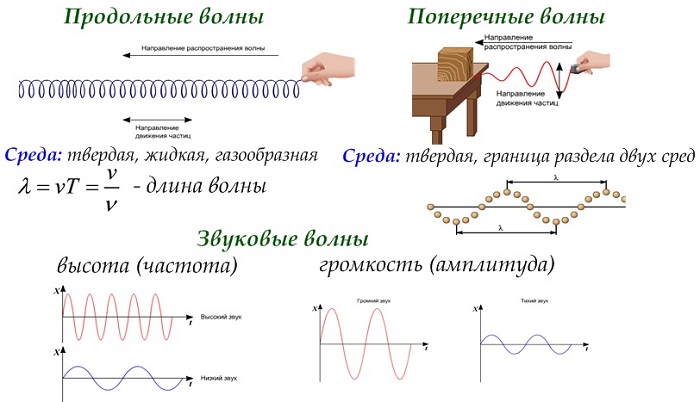
Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.

Греческая буква "λ" (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).

Длинная волна соответствует низкой частоте, а короткая - высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.

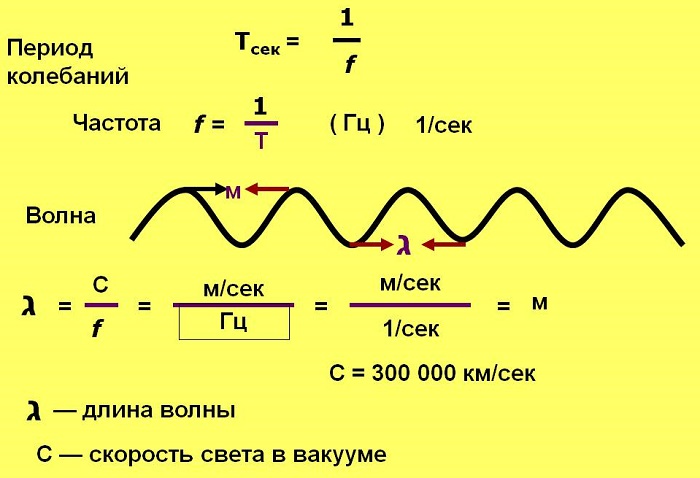
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).

При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).

Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 10 8 м/с поделить на длину в метрах.

Единицы измерения длины волны λ - нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).

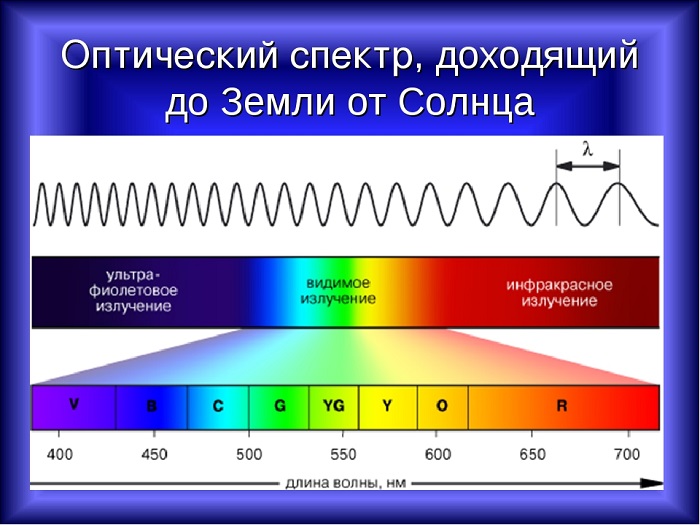
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.

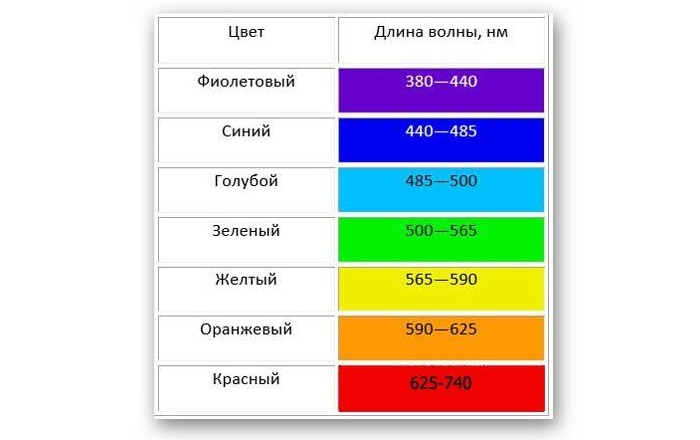
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной - красный, который составляет около 700 нм.

Таблица показывает длину волны в зависимости от цвета:

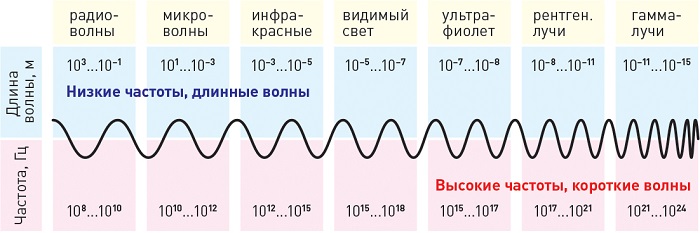
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.

Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.

Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:

Примеры расчета длины волны для звуковых, электромагнитных и радиоволн

Задача №1

Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2

Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3

Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.

Читайте также: